
分析 (1)由题意知a2=1+$\frac{λ-1}{1+1}$,从而可得1+$\frac{λ-1}{1+1}$<1,从而解得0<λ<1;再利用数学归纳法证明0<λ<1时数列{an}单调递减;从而解得;
(2)①化简an+1=$\frac{{a}_{n}+4}{{a}_{n}+1}$为|an+1-2|=$\frac{|{a}_{n}-2|}{{a}_{n}+1}$<|an-2|,从而证明;
②可知|an-2|≤|a1-2|=1,从而可得1≤an≤3,从而可得$\frac{1}{{a}_{n+1}+2}$=$\frac{{a}_{n}+1}{3}$•$\frac{1}{{a}_{n}+2}$≥$\frac{2}{3}$$\frac{1}{{a}_{n}+2}$,$\frac{1}{{a}_{n}+2}$≤$\frac{1}{3}$,从而证明.
解答 解:(1)∵an+1=$\frac{{a}_{n}+λ}{{a}_{n}+1}$,a1=1,λ>0,
∴an>0恒成立;
∴an+1=1+$\frac{λ-1}{{a}_{n}+1}$,故a2=1+$\frac{λ-1}{1+1}$,
∵数列{an}单调递减,
∴1+$\frac{λ-1}{1+1}$<1,
∴0<λ<1;
当0<λ<1时,显然a1>a2,
假设当n=k(k∈N*)时,ak>ak+1,
∴$\frac{1}{{a}_{k}+1}$<$\frac{1}{{a}_{k+1}+1}$,
又∵λ-1<0,
∴$\frac{λ-1}{{a}_{k}+1}$>$\frac{λ-1}{{a}_{k+1}+1}$,
即1+$\frac{λ-1}{{a}_{k}+1}$>1+$\frac{λ-1}{{a}_{k+1}+1}$,
即ak+1>ak+2,
故当n=k+1时也成立;
故数列{an}单调递减;
故0<λ<1;
(2)①证明:∵an+1=$\frac{{a}_{n}+4}{{a}_{n}+1}$,
∴|an+1-2|=|$\frac{{a}_{n}+4}{{a}_{n}+1}$-2|=$\frac{|{a}_{n}-2|}{{a}_{n}+1}$<|an-2|,
故数列{|an-2|}单调递减;
②∵数列{|an-2|}单调递减,
∴|an-2|≤|a1-2|=1,∴1≤an≤3,
∵an+1=$\frac{{a}_{n}+4}{{a}_{n}+1}$,∴an+1+2=$\frac{{a}_{n}+4}{{a}_{n}+1}$+2=$\frac{3({a}_{n}+2)}{{a}_{n}+1}$,
∴$\frac{1}{{a}_{n+1}+2}$=$\frac{{a}_{n}+1}{3}$•$\frac{1}{{a}_{n}+2}$≥$\frac{2}{3}$$\frac{1}{{a}_{n}+2}$,
又∵$\frac{1}{{a}_{1}+2}$=$\frac{1}{3}$,
∴$\frac{1}{{a}_{1}+2}$$+\frac{1}{{a}_{2}+2}$+…+$\frac{1}{{a}_{n}+2}$≥$\frac{\frac{1}{3}(1-(\frac{2}{3})^{n})}{1-\frac{2}{3}}$=1-($\frac{2}{3}$)n,
∵1≤an≤3,∴$\frac{1}{{a}_{n}+2}$≤$\frac{1}{3}$,
∴$\frac{1}{{a}_{1}+2}$$+\frac{1}{{a}_{2}+2}$+…+$\frac{1}{{a}_{n}+2}$≤$\frac{1}{3}$•n=$\frac{n}{3}$;
故1-($\frac{2}{3}$)n≤$\frac{1}{{a}_{1}+2}$$+\frac{1}{{a}_{2}+2}$+…+$\frac{1}{{a}_{n}+2}$≤$\frac{n}{3}$(n∈N*).
点评 本题考查了数学归纳法的应用及讨论的思想应用,同时考查了放缩法的应用及数列的性质的判断与应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
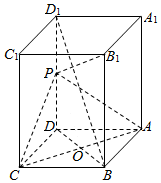 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,点P为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -2+$\sqrt{3}$ | C. | -2-$\sqrt{3}$ | D. | 2±$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | (0,2] | C. | (1,2] | D. | [1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com