练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
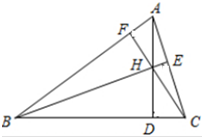
    7．如图，已知△ABC的三条高是AD，BE，CF，用向量方法证明：AD，BE，CF相交于一点．

    分析 设AD，BE相交于一点H，$\overrightarrow{BC}=\overrightarrow{a}$，$\overrightarrow{CA}=\overrightarrow{b}$，$\overrightarrow{CH}=\overrightarrow{h}$，通过向量的数量积证明$\overrightarrow{CH}⊥\overrightarrow{BA}$，得到结果．

    解答 解：设AD，BE相交于一点H，$\overrightarrow{BC}=\overrightarrow{a}$，$\overrightarrow{CA}=\overrightarrow{b}$，$\overrightarrow{CH}=\overrightarrow{h}$，
    则$\overrightarrow{BH}$=$\overrightarrow{a}+\overrightarrow{h}$，$\overrightarrow{AH}$=$\overrightarrow{h}-\overrightarrow{b}$，
    ∵$\overrightarrow{BH}$⊥$\overrightarrow{AC}$，∴$\overrightarrow{BH}$•$\overrightarrow{AC}$=0，∴$（\overrightarrow{a}+\overrightarrow{h}）•\overrightarrow{b}=0$，…①
    同理，$（\overrightarrow{h}-\overrightarrow{b}）•\overrightarrow{a}=0$…②，
    ①+②，$\overrightarrow{h}•\overrightarrow{b}+\overrightarrow{h}•\overrightarrow{a}=0$，∴$\overrightarrow{CH}⊥\overrightarrow{BA}$，
    △ABC的三条高是AD，BE，CF相交于一点．

    点评 本题考查向量在几何中的应用，向量的数量积的运算，考查逻辑推理能力计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．已知正方体ABCD-A1B1C1D1的棱长为1，且点E为棱AB上任意一个动点．当点B1到平面A1EC的距离为$\frac{{\sqrt{21}}}{6}$时，点E所有可能的位置有几个2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知函数f（x）和g（x）是两个定义在区间M上的函数，若对任意的x∈M，存在常数x0∈M，使得f（x）≥f（x0），g（x）≥g（x0），且f（x0）=g（x0），则称函数f（x）和g（x）在区间M上是“相似函数”，若f（x）=|log2（x-1）|+b与g（x）=x3-3x2+8在[$\frac{5}{4}$，3]上是“相似函数”，则函数f（x）在区间[$\frac{5}{4}$，3]上的最大值为（　　）
    A．4B．5C．6D．$\frac{9}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设数列{an}满足a1=1，a1+a2+…+an-1=an-1（n≥2，n∈N*）．
    （1）求数列{an}的通项公式；
    （2）若数列{an}满足logabn=an（a＞1），求证：$\frac{a}{{a}^{2}-1}$≤$\frac{{b}_{1}}{{b}_{2}-1}$+$\frac{{b}_{2}}{{b}_{3}-1}$+…+$\frac{{b}_{n-1}}{{b}_{n}-1}$$＜\frac{1}{a-1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图，折线AOB为一条客机的飞机航线，其中OA、OB夹角为$\frac{2π}{3}$，若一架客机沿A-O-B方向飞行至距离O点90km处的C点时，发现航线转折点O处开始产生一个圆形区域的高压气旋，高压气旋范围内的区域为危险区域（含边界），为了保证飞行安全，客机航线需临时调整为CD，若CD与OA的夹角为θ，D在OB上，已知客机的飞行速度为15km/min．
    （1）当飞机在临时航线上飞行t分钟至点E时，试用t和θ表示飞机到O点的距离OE；
    （2）当飞机在临时航线上飞行t分钟时，高压气旋半径r=3t$\sqrt{t}$km，且半径增大到81km时不再继续增大，若CD与OA的夹角θ=$\frac{π}{4}$，试计算飞机在临时航线CD上是否能安全飞行．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知椭圆$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1过其右焦点F的直线l与椭圆相交于A、B两点，若点P为（4，0），设$\overrightarrow{FA}=λ\overrightarrow{FB}$，λ∈[-2，-1]，求|$\overrightarrow{PA}+\overrightarrow{PB}$|取最大值时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．如图所示的是一多面体的三视图（尺寸如图所示，单位：cm），则它的表面积是（　　）
    A．（6+3$\sqrt{3}$）cm2B．（12+3$\sqrt{3}$）cm2C．15cm2D．9cm2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知点F（1，0），点P为平面上的动点，过点P作直线l：x=-1的垂线，垂足为H，且$\overrightarrow{HP}$•$\overrightarrow{HF}$=$\overrightarrow{FP}$•$\overrightarrow{FH}$．
    （1）求动点P的轨迹C的方程；
    （2）设点P的轨迹C与x轴交于点M，点A，B是轨迹C上异于点M的不同D的两点，且满足$\overrightarrow{MA}$•$\overrightarrow{MB}$=0，在A，B处分别作轨迹C的切线交于点N，求点N的轨迹E的方程；
    （3）在（2）的条件下，求证：kMN•kAB为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）过点（1，$\frac{{\sqrt{3}}}{2}$），离心率为$\frac{{\sqrt{3}}}{2}$．过椭圆右顶点A的两条斜率乘积为-$\frac{1}{4}$的直线分别交椭圆C于M，N两点．
    （Ⅰ）求椭圆C的标准方程；
    （Ⅱ）直线MN是否过定点D？若过定点D，求出点D的坐标；若不过，请说明理由．

    查看答案和解析>>

    同步练习册答案