
分析 (1)利用抛物线的定义,求出p,即可求抛物线C的方程;
(2)证明线段CD被线段PQ平分,即可证明四边形PCQD是平行四边形.
解答  (1)解:因为$|{MF}|=4+\frac{p}{2}=6$
(1)解:因为$|{MF}|=4+\frac{p}{2}=6$
所以p=4,即抛物线C的方程是x2=8y…(3分)
(2)证明:由x2=8y得$y=\frac{x^2}{8}$,${y^'}=\frac{x}{4}$…(4分)
设$A({{x_1},\frac{x_1^2}{8}}),B({{x_2},\frac{x_2^2}{8}})$,
则直线PA的方程为$y-\frac{x_1^2}{8}=\frac{x_1}{4}({x-{x_1}})$,①…(5分)
则直线PB的方程为$y-\frac{x_2^2}{8}=\frac{x_2}{4}({x-{x_2}})$,②…(6分)
由①和②解得:$x=\frac{{{x_1}+{x_2}}}{2},y=\frac{{{x_1}{x_2}}}{8}$,所以$P({\frac{{{x_1}+{x_2}}}{2},\frac{{{x_1}{x_2}}}{8}})$…(7分)
设点Q(0,t),则直线AB的方程为y=kx+t…(8分)
由$\left\{\begin{array}{l}{x^2}=8y\\ y=kx+t\end{array}\right.$得x2-8kx-8t=0
则x1+x2=8k,x1x2=-8t…(9分)
所以P(4k,-t),所以线段PQ被x轴平分,即被线段CD平分,
在①中,令y=0解得$x=\frac{x_1}{2}$,所以$C({\frac{x_1}{2},0})$,同理得$D({\frac{x_2}{2},0})$,所以线段CD的中点
坐标为$({\frac{{{x_1}+{x_2}}}{4},0})$,即(2k,0)…(10分)
又因为直线PQ的方程为$y=-\frac{t}{2k}x+t$,所以线段CD的中点(2k,0)在直线PQ上,
即线段CD被线段PQ平分…(11分)
因此,四边形PCQD是平行四边形…(12分)
点评 本题考查抛物线的定义与方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (4,-4,6) | B. | (-6,-6,-5) | C. | (10,0,7) | D. | (10,-6,19) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
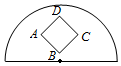 如图,在半径为1的半圆内,放置一个边长为$\frac{1}{2}$的正方形ABCD,向半圆内任取一点,则该点落在正方形内的槪率为( )
如图,在半径为1的半圆内,放置一个边长为$\frac{1}{2}$的正方形ABCD,向半圆内任取一点,则该点落在正方形内的槪率为( )| A. | $\frac{1}{π}$ | B. | $\frac{1}{2π}$ | C. | $\frac{2}{π}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
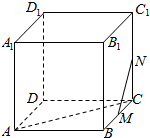 如图,正方体ABCD-A1B1C1D1中,M,N分别为棱BC,CC1的中点,则异面直线AC和MN所成角的大小为( )
如图,正方体ABCD-A1B1C1D1中,M,N分别为棱BC,CC1的中点,则异面直线AC和MN所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com