Question

20．函数f（x）=$\left\{\begin{array}{l}{|lnx-1|，x＞0}\\{-{x}^{2}-2x+2，x≤0}\end{array}\right.$，若f（a）=f（b）=f（c）=f（d）且a＜b＜c＜d，给出下列三个结论：
①abcd∈（0，e²]；
②a+b+c+d∈（e³+$\frac{1}{e}$-2，e⁴+$\frac{1}{{e}^{2}}$-2]；
③已知关于x的方程f（x）+（-1）^kx-t=0恰有三个不同实根，若k为偶数，则t∈[2，$\frac{9}{4}$]；若k为奇数，则t=[2，$\frac{17}{4}$]；其中正确的结论有（　　）个．

• A． 0
• B． 1
• C． 2
• D． 3

Answer 1

分析 画出函数f（x）=$\left\{\begin{array}{l}{|lnx-1|，x＞0}\\{-{x}^{2}-2x+2，x≤0}\end{array}\right.$的图象，数形结合，分析三个结论的真假，可得答案．

解答 解：∵f（x）=$\left\{\begin{array}{l}{|lnx-1|，x＞0}\\{-{x}^{2}-2x+2，x≤0}\end{array}\right.$=$\left\{\begin{array}{l}-（x+1）^{2}+3，x≤0\\ 1-lnx，0＜x＜1\\ lnx-1，x≥1\end{array}\right.$
∴函数f（x）的图象如下图所示：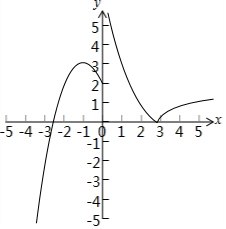

若直线y=m与函数f（x）的图象相交于四个不同的点，由图可知m∈[2，3），
则a，b是x²+2x+m-2=0
的两根，∴a+b=-2，ab=m-2，
∴ab∈[0，1），且lnc=1-m，lnd=1+m，
∴ln（cd）=2，
∴cd=e²，
∴abcd∈[0，e²），
∴①是正确的．
由1-lnx=3得x=$\frac{1}{{e}^{2}}$，由1-lnx=2得x=$\frac{1}{e}$，
∴c∈（$\frac{1}{{e}^{2}}$，$\frac{1}{e}$]，又∵cd=e²，
∴a+b+c+d=c+$\frac{{e}^{2}}{c}$-2在（$\frac{1}{{e}^{2}}$，$\frac{1}{e}$]是递减函数，∴a+b+c+d∈∈[e³+$\frac{1}{e}$-2，e⁴+$\frac{1}{{e}^{2}}$-2）；
∴②是错误的
已知关于x的方程f（x）+（-1）^kx-t=0恰有三个不同实根，若k为偶数，
即f（x）+x-t=0恰有三个不同实根，
则y=f（x）与y=-x+t有三个不同的交点，
当y=-x+t过（0，2）点时，t=2，
当y=-x+t与抛物线相切时，-x+t=-x²-2x+2，即x²+x+t-2=0的△=1-4（t-2）=0，
解得：t=$\frac{9}{4}$，
故t∈[2，$\frac{9}{4}$]；
若k为奇数，即f（x）-x-t=0恰有三个不同实根，
则y=f（x）与y=x+t有三个不同的交点，
当y=x+t过（0，2）点时，t=2，
当y=x+t与抛物线相切时，x+t=-x²-2x+2，即x²+3x+t-2=0的△=9-4（t-2）=0，
解得：t=$\frac{17}{4}$，
故t∈[2，$\frac{17}{4}$]；
若关于x的方程f（x）+x=m恰有三个不同实根，则y=f（x）与y=-x+m有三个不同的交点，
故③正确的
故选C

点评 本题考查函数的图象，分段函数，零点与方程的根之间的关系，综合性较强．