
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |
 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,
时, 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围. (1)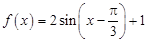 ;(2)实数
;(2)实数 的取值范围为
的取值范围为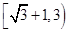 .
.
解析试题分析:(1)根据表格提供的数据,求出周期T,注意:三角函数的周期等于图象上相邻两个最低点的横坐标之差的绝对值,解出ω,由A>0知函数的最大值为A+B,最小值为-A+B,利用已知最小值、最大值可求出A、B,结合周期求出φ,可求函数 的一个解析式.
的一个解析式.
(2)函数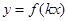 (k>0)周期为
(k>0)周期为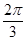 ,求出k,x∈[0,
,求出k,x∈[0, ],推出3x?
],推出3x? 的范围,画出图象,数形结合容易求出m的范围.
的范围,画出图象,数形结合容易求出m的范围.
试题解析:(1)设 的最小正周期为
的最小正周期为 ,得
,得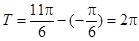 , 2分
, 2分
由 , 得
, 得 ,又
,又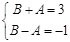 ,解得
,解得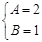 4分
4分
令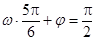 ,即
,即 ,解得
,解得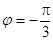 , 5分
, 5分
∴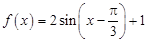 6分
6分
(2)∵函数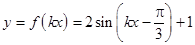 的周期为
的周期为 ,
,
又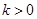 , ∴
, ∴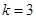 , 7分
, 7分
令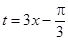 ,∵
,∵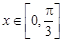 , ∴
, ∴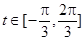 , .8分
, .8分
如图,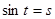 在
在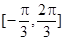 上有两个不同的解,则
上有两个不同的解,则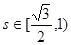 , 10分
, 10分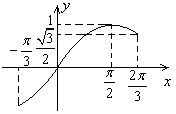
∴方程 在
在 时恰好有两个不同的解,
时恰好有两个不同的解,
则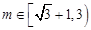 ,即实数
,即实数 的取值范围是
的取值范围是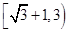 12分
12分
考点:1.由三角函数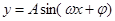 的部分图象求解析式;2.三角函数的周期性及求法.
的部分图象求解析式;2.三角函数的周期性及求法.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com