
分析 (1)利用三角恒等变换,化简函数f(x)的解析式,利用函数y=Asin(ωx+φ)的基本性质,得出结论.
(2)用五点法作出它一个周期内的图象.
(3)利用f(x)=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)的图象变换规律,得出结论.π
(4)利用正弦函数的定义域和值域,求得f(x)的值域.
解答 解:∵函数f(x)=sin2(x+$\frac{π}{4}$)+cos2x-1=$\frac{1-cos(2x+\frac{π}{2})}{2}$+$\frac{1+cos2x}{2}$-1=$\frac{1+sin2x}{2}$+$\frac{1+cos2x}{2}$-1=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$),
(1)故f(x)的最小正周期为$\frac{2π}{2}$=π、振幅为$\frac{\sqrt{2}}{2}$、初相为$\frac{π}{4}$.
令2x+$\frac{π}{4}$=kπ,k∈Z,求得x=$\frac{kπ}{2}$-$\frac{π}{8}$,可得f(x)的图象的对称中心为 ($\frac{kπ}{2}$-$\frac{π}{8}$,0).
(2)用五点法作出它一个周期内的图象,
列表:
| x | -$\frac{π}{8}$ | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ |
| 2x+$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 0 | $\frac{\sqrt{2}}{2}$ | 0 | -$\frac{\sqrt{2}}{2}$ | 0 |
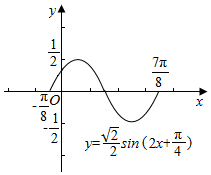
点评 本题主要考查三角恒等变换,函数y=Asin(ωx+φ)的基本性质,用五点法作出f(x)=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)在一个周期内的图象以及它的图象变换规律,正弦函数的定义域和值域,属于中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 若z1、z2∈C,z1-z2>0,则z1>z2 | B. | 若z∈R,则z•$\overline{z}$=|z|2不成立 | ||
| C. | z1、z2∈C,z1•z2=0,则z1=0或z2=0 | D. | z1、z2∈C,z12+z22=0,则z1=0且z2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{2}{3}$)∪($\frac{4}{3}$,+∞) | B. | ($\frac{2}{3}$,$\frac{4}{3}$) | C. | (-∞,$\frac{1}{3}$)∪($\frac{2}{3}$,+∞) | D. | ($\frac{1}{3}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $2+2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1BC的底面△ABC中,CA=CB=2,∠BCA=90°,棱AA1=4,M.N分别是A1B1,A1A的中点.
如图,在直三棱柱ABC-A1BC的底面△ABC中,CA=CB=2,∠BCA=90°,棱AA1=4,M.N分别是A1B1,A1A的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正方形的直观图是正方形? | |
| B. | 平行四边形的直观图是平行四边形? | |
| C. | 有两个面平行,其余各面都是平行四边形的几何体叫棱柱 | |
| D. | 用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com