
现有0,1,2,3,4,5六个数字。
(1)用所给数字能够组成多少个四位数?
(2)用所给数字可以组成多少个没有重复数字的五位数?
(3)用所给数字可以组成多少个没有重复数字且比3142大的数?
(最后结果均用数字作答)
(1)1080,(2)600,(3)1360.
解析试题分析:(1)四位数要求首位不为零,根据特殊元素、特殊位置优先考虑的原则,先排首位有5种选择,后三位由于可重复,各有6种选择. 能够组成四位数的个数为:5×6×6×6=1080,(2)同样可得:能组成没有重复数字的五位数的个数为: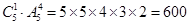 ,(3)分类讨论:比3142大的数包含四位数、五位数和六位数,其中:六位数有:
,(3)分类讨论:比3142大的数包含四位数、五位数和六位数,其中:六位数有: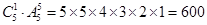 ,五位数有:
,五位数有: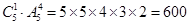 ,四位数又要分有千位是4或5的,千位是3的,而千位是4或5的有
,四位数又要分有千位是4或5的,千位是3的,而千位是4或5的有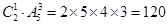 ;千位是3的分为百位是2、4、5的与百位是1的,百位是2、4、5的有
;千位是3的分为百位是2、4、5的与百位是1的,百位是2、4、5的有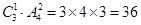 ,百位是1的分为十位是4和5两种情况,十位是5的有3种,十位是4的有1种,所以共有600+600+120+36+3+1=1360.
,百位是1的分为十位是4和5两种情况,十位是5的有3种,十位是4的有1种,所以共有600+600+120+36+3+1=1360.
试题解析:(1)能够组成四位数的个数为:5×6×6×6=1080 5分;
(2)能组成没有重复数字的五位数的个数为: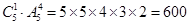 ;10分
;10分
(3)比3142大的数包含四位数、五位数和六位数,其中:
六位数有: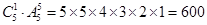 ;
;
五位数有: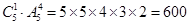 ;
;
四位数有千位是4或5的,千位是3的,而千位是4或5的有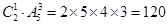 ;千位是3的分为百位是2、4、5的与百位是1的,
;千位是3的分为百位是2、4、5的与百位是1的,
百位是2、4、5的有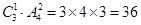 ,
,
百位是1的分为十位是4和5两种情况,十位是5的有3种,十位是4的有1种,
所以共有600+600+120+36+3+1=1360。 15分
答:能组成四位数1080个;没有重复数字的五位数600个;比3142大的数1360个。 16分
(要求解答过程要有必要的文字说明及运算公式,若没有视具体情况酌情扣分)
考点:排列组合


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
设有5幅不同的国画,2幅不同的油画,7幅不同的水彩画.
(1)从这些国画、油画、水彩画中各选一幅画布置房间,有几种不同的选法?
(2)从这些画中任选出两幅不同画种的画布置房间,有几种不同的选法?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
7个人排成一排,按下列要求各有多少种排法?
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙、丙3人必须相邻;
(3)其中甲、乙、丙3人两两不相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲、乙、丙按从左到右的顺序排列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知(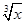 +x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-
+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-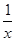 )2n的展开式中:
)2n的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从5名女同学和4名男同学中选出4人参加演讲比赛,分别按下列要求,各有多少种不同的选法?
(1)男、女同学各2名;
(2)男、女同学分别至少有1名;
(3)在(2)的前提下,男同学甲与女同学乙不能同时选出.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com