Question

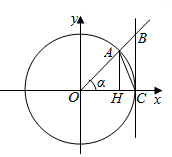
1．如图所示，在单位圆O中，∠AOH=α（0＜α＜$\frac{π}{2}$），若△AOH的面积记为S₁，△BOC的面积记为S₂，△AOC的面积为S₃，扇形AOC的面积记为S₄，则（　　）

• A． S₁=$\frac{1}{2}$sinα
• B． S₂=$\frac{1}{2}$tanα
• C． S₃=α
• D． S₄=$\frac{1}{2}$cosα

Answer 1

分析 利用单位圆，三角函数线，以及三角形面积公式，扇形面积公式即可分别求其面积，即可得解．

解答 解：∵在单位圆O中，∠AOH=α（0＜α＜$\frac{π}{2}$），
∴△AOH的面积记为S₁=$\frac{1}{2}OH•AH$=$\frac{1}{2}$sinαcosα；
△BOC的面积记为S₂=$\frac{1}{2}×1×BC$=$\frac{1}{2}$tanα，
△AOC的面积为S₃=$\frac{1}{2}×$OC×AH=$\frac{1}{2}×1×$sinα=$\frac{1}{2}$sinα；
扇形AOC的面积记为S₄=$\frac{1}{2}×$1²×α=$\frac{1}{2}$α．
比较各个选项，B正确．
故选：B．

点评 本题主要考查了单位圆，三角函数线，以及三角形面积公式，扇形面积公式的综合应用，考查了数形结合思想的应用，属于基础题．