
分析 二项式($\frac{x}{3}$+$\frac{3}{x}$)10的展开式的通项公式Tr+1=${∁}_{10}^{r}$$(\frac{x}{3})^{10-r}$$(\frac{3}{x})^{r}$=32r-10${∁}_{10}^{r}$x10-2r,令10-2r=0,解得r即可得出.
解答 解:二项式($\frac{x}{3}$+$\frac{3}{x}$)10的展开式的通项公式Tr+1=${∁}_{10}^{r}$$(\frac{x}{3})^{10-r}$$(\frac{3}{x})^{r}$=32r-10${∁}_{10}^{r}$x10-2r,
令10-2r=0,解得r=5.
∴二项式($\frac{x}{3}$+$\frac{3}{x}$)10的展开式中不含x的项第6项:${∁}_{10}^{5}$,即252.
故答案为:第6项,即252.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
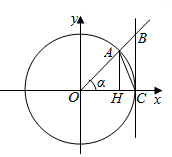 如图所示,在单位圆O中,∠AOH=α(0<α<$\frac{π}{2}$),若△AOH的面积记为S1,△BOC的面积记为S2,△AOC的面积为S3,扇形AOC的面积记为S4,则( )
如图所示,在单位圆O中,∠AOH=α(0<α<$\frac{π}{2}$),若△AOH的面积记为S1,△BOC的面积记为S2,△AOC的面积为S3,扇形AOC的面积记为S4,则( )| A. | S1=$\frac{1}{2}$sinα | B. | S2=$\frac{1}{2}$tanα | C. | S3=α | D. | S4=$\frac{1}{2}$cosα |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{11}{6}$] | B. | [$\frac{1}{2}$,$\frac{11}{6}$) | C. | ($\frac{1}{3}$,$\frac{13}{6}$] | D. | [$\frac{1}{3}$,$\frac{13}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com