
分析 由条件利用诱导公式、两角和差的三角公式,求得要求式子的值.
解答 解:sin410°cos145°+sin680°sin(-35°)=sin50°(-cos35°)+sin(-40°)sin(-35°)
=-sin50°cos35°+sin40°sin35°=-sin50°cos35°+cos50°sin35°
=sin(35°-50°)=-sin15°=-sin(45°-30°)=-(sin45°cos30°-cos45°sin30°)
-($\frac{\sqrt{2}}{2}•\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}•\frac{1}{2}$)=$\frac{\sqrt{2}-\sqrt{6}}{4}$,
故答案为:$\frac{\sqrt{2}-\sqrt{6}}{4}$.
点评 本题主要考查诱导公式、两角和差的三角公式的应用,属于基础题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
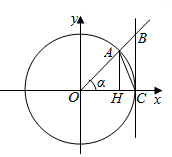 如图所示,在单位圆O中,∠AOH=α(0<α<$\frac{π}{2}$),若△AOH的面积记为S1,△BOC的面积记为S2,△AOC的面积为S3,扇形AOC的面积记为S4,则( )
如图所示,在单位圆O中,∠AOH=α(0<α<$\frac{π}{2}$),若△AOH的面积记为S1,△BOC的面积记为S2,△AOC的面积为S3,扇形AOC的面积记为S4,则( )| A. | S1=$\frac{1}{2}$sinα | B. | S2=$\frac{1}{2}$tanα | C. | S3=α | D. | S4=$\frac{1}{2}$cosα |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{11}{6}$] | B. | [$\frac{1}{2}$,$\frac{11}{6}$) | C. | ($\frac{1}{3}$,$\frac{13}{6}$] | D. | [$\frac{1}{3}$,$\frac{13}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com