
分析 利用导数求出切线方程,根据定积分的计算公式求得S=${∫}_{0}^{1}$x2dx=$\frac{1}{12}$.
解答 解:y'=2x,所以抛物线在x=1处切线斜率为2,切点(1,1),
故切线方程为y-1=2(x-1),即y=2x-1,切线交x轴于点$({\frac{1}{2},0})$,
所以抛物线y=x2及其在x=1处切线和x轴围成的图形的面积为:
S=$\int_0^1{{x^2}dx}-\frac{1}{2}×\frac{1}{2}×1=\frac{1}{3}{x^3}\left|\begin{array}{l}1\\ 0\end{array}\right.-\frac{1}{4}=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}$,
故答案为:$\frac{1}{12}$.
点评 本题考查利用导数法求函数的切线方程,利用定积分求围成图形的面积,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 42种 | B. | 36种 | C. | 30种 | D. | 25种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {0,1} | C. | {-1,0,1} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin(α+β)=cosαsinβ+sinαcosβ | B. | cos(α+β)=cosαcosβ+sinαsinβ | ||
| C. | sin(α-β)=cosαsinβ-sinαcosβ | D. | cos(α-β)=cosαcosβ-sinαsinβ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
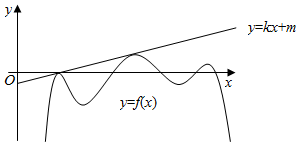
| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com