
 一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)
一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示) 分析 如图,设圆的半径为r,设底角B=2α,由条件利用直角三角形中的边角关系,求得tanα的值,可得2α的值.
解答 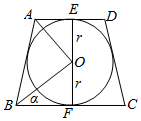 解:∵一个圆内切于一个等腰锑形,设圆的半径为r,设底角B=2α,
解:∵一个圆内切于一个等腰锑形,设圆的半径为r,设底角B=2α,
则A=180°-2α,故∠OBF=α,∠OAE=90°-α,
∴BC=2BF=2r•cotα,AD=2AE=2r•cot(90°-α).
∵已知圆面积是等腰锑形面积的$\frac{1}{2}$,∴$\frac{1}{2}$(AD+BC)•2r=2•π•r2,
即[2r•cot(90°-α)+2r•cotα]•r=2•π•r2,
求得tanα+cotα=π,∴tanα=$\frac{π-\sqrt{{π}^{2}-4}}{2}$,∴α=arctan$\frac{π-\sqrt{{π}^{2}-4}}{2}$,
故等腰梯形的底角B=2α=2arctan$\frac{π-\sqrt{{π}^{2}-4}}{2}$.
点评 本题主要考查直角三角形中的边角关系,反三角函数的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-9,1) | B. | (9,-1) | C. | (9,1) | D. | (-9,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | 2 | D. | $\frac{2+2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 乙 | 丙 | 丁 | |
| 耐力成绩(X) | 7.5 | m | 8 | 8.5 |
| 体能成绩(Y) | 8 | n | 8.5 | 9.5 |
| 体质成绩(X+Y) | 15.5 | 16 | 16.5 | 18 |
| 体质健康优秀 | 体质健康不优秀 | 总计 | |
| 心肺功能优秀 | 18 | 9 | 27 |
| 心肺功能不优秀 | 8 | 15 | 23 |
| 总计 | 26 | 24 | 50 |
| P(K2>k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
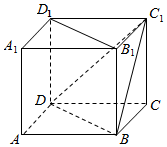 如图,ABCD-A1B1C1D1为正方体.
如图,ABCD-A1B1C1D1为正方体.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com