
分析 根据等比数列的通项公式化简已知的两条件a1+a3=30和S4=120,得到关于首项和公比的方程组,求出方程组的解即可得到首项和公比,根据求出的首项和公比写出等比数列{an}的通项公式,把写出的通项公式代入到bn=1+log3an中,利用对数的运算法则计算后,得到bn的通项公式.
解答 解:设等比数列的公比为q,由a1+a3=30,S4=120,
得到$\left\{\begin{array}{l}{{a}_{1}(1+{q}^{2})=30①}\\{\frac{{a}_{1}(1-{q}^{4})}{1-q}=120②}\end{array}\right.$,
由②得:$\frac{{a}_{1}(1+{q}^{2})(1-q)(1+q)}{1-q}$=a1(1+q2)(1+q)=120③,
把①代入③得:1+q=4,解得q=3,把q=3代入①得到a1=3,
则等比数列{an}的通项公式为:an=3n,
将通项公式代入bn=1+log3an中,得bn=n+1,
故答案是:bn=n+1.
点评 此题考查学生灵活运用等比数列的通项公式化简求值,掌握对数的运算法则,是一道中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
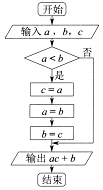
| A. | 若输入a,b,c的值依次为1,2,3,则输出的值为5 | |
| B. | 若输入a,b,c的值依次为1,2,3,则输出的值为7 | |
| C. | 若输入a,b,c的值依次为2,3,4,则输出的值为8 | |
| D. | 若输入a,b,c的值依次为2,3,4,则输出的值为10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com