
【题目】在平面直角坐标系![]() 中,动圆
中,动圆![]() 经过点
经过点![]() 并且与直线
并且与直线![]() 相切,设动圆
相切,设动圆![]() 圆心的轨迹为曲线
圆心的轨迹为曲线![]() .
.
(1)如果直线![]() 过点(0,4),且和曲线
过点(0,4),且和曲线![]() 只有一个公共点,求直线
只有一个公共点,求直线![]() 的方程;
的方程;
(2)已知不经过原点的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,判断命题“如果
两点,判断命题“如果![]() ,那么直线
,那么直线![]() 经过点
经过点![]() ”是真命题还是假命题,并说明理由.
”是真命题还是假命题,并说明理由.
【答案】(1)直线![]() 的方程为
的方程为![]() 、
、![]() 、
、![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据抛物线的定义,求得曲线C的方程,之后分直线的斜率存在与不存在两种情况,根据直线与抛物线有一个公共点,得出结果;
(2)根据图形的对称性,得出对应的定点在x轴上,设出直线的方程,利用韦达定理,根据向量垂直向量的数量积等于零,求得对应的结果.
(1)根据题意,可知曲线C的方程为![]() ,
,
①直线![]() 的斜率不存在,即
的斜率不存在,即![]() 的方程为
的方程为![]() ,符合题意,
,符合题意,
②直线![]() 的斜率存在,设
的斜率存在,设![]() ,
,
与抛物线方程联立得![]() ,
,
(ⅰ)![]() ,符合题意,此时
,符合题意,此时![]() 的方程为
的方程为![]() ,
,
(ⅱ)![]() ,则
,则![]() ,解得
,解得![]() ,此时
,此时![]() 的方程为
的方程为![]() ,
,
综上,符合题意的直线![]() 的方程为
的方程为![]() 、
、![]() 、
、![]() ;
;
(2)由图形的对称性,若直线![]() 过定点,则该定点必定落在
过定点,则该定点必定落在![]() 轴上,
轴上,
设定点坐标为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
∴命题为真命题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.

(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤![]() (x+2)2成立.
(x+2)2成立.
(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
(3)设g(x)=f(x)-![]() x,x∈[0,+∞),若g(x)图象上的点都位于直线y=
x,x∈[0,+∞),若g(x)图象上的点都位于直线y=![]() 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(1)若![]() ,
,![]() ,求△
,求△![]() 的面积;
的面积;
(2)过点![]() 作圆O的两条切线,切点分别为E,F,求
作圆O的两条切线,切点分别为E,F,求![]() ;
;
(3)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
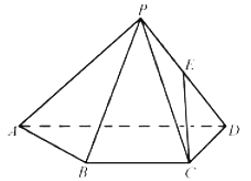
【题目】如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1的棱长为2,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的三视图的面积之和最大值为( )

A.6B.7C.8D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位决定投资![]() 元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每
元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每![]() 长造价
长造价![]() 元,两侧墙砌砖,每
元,两侧墙砌砖,每![]() 长造价
长造价![]() 元,
元,
(1)求该仓库面积![]() 的最大值;
的最大值;
(2)若为了使仓库防雨,需要为仓库做屋顶.顶部每![]() 造价
造价![]() 元,求仓库面积
元,求仓库面积![]() 的最大值,并求出此时正面铁栅应设计为多长?
的最大值,并求出此时正面铁栅应设计为多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车收费标准如下:起步价![]() 元,起步历程为
元,起步历程为![]() (不超过
(不超过![]() 按起步价付费);超过
按起步价付费);超过![]() 但不超过
但不超过![]() ,超过部分按每千米
,超过部分按每千米![]() 元收费;超过
元收费;超过![]() 时,超过部分按每千米
时,超过部分按每千米![]() 元收费;另外每次乘坐需付燃油附加费
元收费;另外每次乘坐需付燃油附加费![]() 元.
元.
(1)写出乘车费用![]() (元)关于路程
(元)关于路程![]() (千米)的函数关系式;
(千米)的函数关系式;
(2)若某人一次出租车费用为31.15元,求此次出租车行驶了多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com