
分析 利用同角三角函数的基本关系,两角差的三角公式,化简等式的左边,可得结论.
解答 证明:∵已知$\frac{tan(α-γ)}{tanα}$+$\frac{si{n}^{2}β}{si{n}^{2}α}$=1,∴$\frac{sin(α-γ)cosα}{sinαcos(α-γ)}$+$\frac{{sin}^{2}β}{{sin}^{2}α}$=1,
∴sin2β=sin2α•[1-$\frac{sin(α-γ)cosα}{cos(α-γ)sinα}$]=sin2α•$\frac{cos(α-γ)sinα-sin(α-γ)cosα}{cos(α-γ)sinα}$=$\frac{{sin}^{2}αcos(α-γ)-sinαcosαsin(α-γ)}{cos(α-γ)}$
=sinα•$\frac{sin[α-(α-γ)]}{cos(α-γ)}$=$\frac{sinαsinγ}{cos(α-γ)}$=$\frac{sinαsinγ}{cosαcosγ+sinαsinγ}$.
∵tan2β=$\frac{{sin}^{2}β}{1{-sin}^{2}β}$=$\frac{\frac{sinαsinγ}{cosαcosγ+sinαsinγ}}{1-\frac{sinαsinγ}{cosαcosγ+sinαsinγ}}$=$\frac{sinαsinγ}{cosαcosγ}$=tanα•tanγ,
∴tan2β=tanαtanγ成立.
点评 本题主要考查同角三角函数的基本关系,两角差的三角公式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
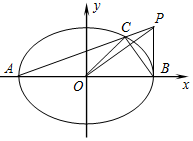 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右顶点分别是A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),离心率为$\frac{{\sqrt{2}}}{2}$.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右顶点分别是A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),离心率为$\frac{{\sqrt{2}}}{2}$.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 1.5 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列1,3,5,7与7,5,3,1是同一数列 | |
| B. | 数列0,1,2,3,…的通项公式是an=n | |
| C. | -1,1,-1,1,…是常数列 | |
| D. | 1,2,22,23,…是递增数列,也是无穷数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{e}$,e] | B. | [-$\frac{2}{e}$,2e] | C. | (-$\frac{2}{e}$,2e) | D. | [-$\frac{3}{e}$,3e] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com