
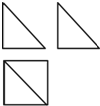
 利用一球体毛坯切削后得到一个几何体,该几何体的三视图如图所示,若主视图和左视图都是直角边长为1的等腰直角三角形,则毛坯球体的体积最小应为( )
利用一球体毛坯切削后得到一个几何体,该几何体的三视图如图所示,若主视图和左视图都是直角边长为1的等腰直角三角形,则毛坯球体的体积最小应为( )| A. | $\frac{{\sqrt{2}π}}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{\sqrt{3}π}{2}$ | D. | $\frac{8\sqrt{2}π}{3}$ |
分析 根据几何体的三视图,得出该几何体是有一条侧棱垂直于底面的四棱锥,
将其补全为一个正方体,得出正方体为球的内接正方体时球的体积最小,由此求出球的体积.
解答 解:由几何体的三视图知,该几何体是一个有一条侧棱垂直于底面的四棱锥,
将这个四棱锥补全为一个正方体,则:
当正方体为球的内接正方体时球的体积最小,
此时正方体的体对角线为球的直径,
长为2R=$\sqrt{{1}^{2}{+1}^{2}{+1}^{2}}$=$\sqrt{3}$,
所以球的体积为:
$V=\frac{4}{3}π{(\frac{{\sqrt{3}}}{2})^3}=\frac{{\sqrt{3}}}{2}π$.
故选:C.
点评 本题考查了空间几何体的三视图的应用问题,解题的关键是由三视图得出几何体的结构特征,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 4x-y+10=0 | B. | 4x-y+2=0 | C. | x-4y+10=0 | D. | x-4y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
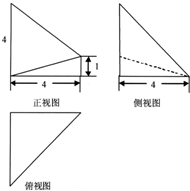
| A. | $\frac{40}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{28}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
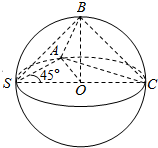 已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{5\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com