
分析 (1)求出h'(x)=(x+1)ex,利用导数性质能求出x=-1时,h(x)取得最小值$-\frac{1}{e}$.
(2)设t(x)=f(x)-g(x)=ex-lnx-a,则$t'(x)={e^x}-\frac{1}{x}=\frac{{x{e^x}-1}}{x}({x>0})$,推导出存在${x_0}∈({\frac{1}{2},1})$使得T(x0)=0,求出t(x))的最小值为$t({x_0})={e^{x_0}}-ln{x_0}-a=0$,由此能证明曲线y=f(x)与y=g(x)在P点处有相同的切线,并能求出$a∈({2,\frac{5}{2}})$.
解答 解:(1)∵f(x)=ex,∴h(x)=xf(x)=xex,
∴h'(x)=(x+1)ex,
当x<-1时,h'(x)<0,h(x)单调递减;
当x>-1时,h'(x)>0,h(x)单调递增,
故x=-1时,h(x)取得最小值$-\frac{1}{e}$.
证明:(2)∵g(x)=lnx+a.
∴设t(x)=f(x)-g(x)=ex-lnx-a,则$t'(x)={e^x}-\frac{1}{x}=\frac{{x{e^x}-1}}{x}({x>0})$,
由(1)得T(x)=xex-1在(0,+∞)单调递增,又$T({\frac{1}{2}})<0$,T(1)>0,
∴存在${x_0}∈({\frac{1}{2},1})$使得T(x0)=0,
∴当x∈(0,x0)时,t'(x)<0,t(x)单调递减;
当x∈(x0,+∞)时,t'(x)>0,t(x)单调递增,
∴t(x))的最小值为$t({x_0})={e^{x_0}}-ln{x_0}-a=0$,
由T(x0)=0得${e^{x_0}}=\frac{1}{x_0}$,
∴曲线y=f(x)与y=g(x)在P点处有相同的切线,
又$a={e^{x_0}}-ln{x_0}$,∴$a=\frac{1}{x_0}+{x_0}$,
∵${x_0}∈({\frac{1}{2},1})$,∴$a∈({2,\frac{5}{2}})$.
点评 本题考查函数的最小值的求法,考查曲线y=f(x)与y=g(x)在点P处有相同的切线,且$a∈({2,\frac{5}{2}})$的证明,考查导数性质、构造法、函数单调性等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
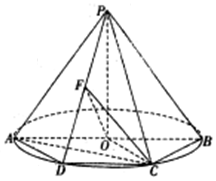 如图,AB是圆O的直径,点C,D是圆O上异于A,B的点,CD∥AB,F为PD中点,PO⊥垂直于圆O所在的平面,∠ABC=60°.
如图,AB是圆O的直径,点C,D是圆O上异于A,B的点,CD∥AB,F为PD中点,PO⊥垂直于圆O所在的平面,∠ABC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
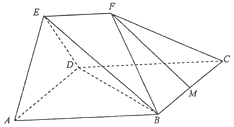 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:解答题
从3名男生和2名女生中任选两人参加演讲比赛,试求:
(1)所选2人都是男生的概率;
(2)所选2人恰有1名女生的概率;
(3)所选2人至少有1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com