
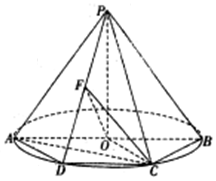
 如图,AB是圆O的直径,点C,D是圆O上异于A,B的点,CD∥AB,F为PD中点,PO⊥垂直于圆O所在的平面,∠ABC=60°.
如图,AB是圆O的直径,点C,D是圆O上异于A,B的点,CD∥AB,F为PD中点,PO⊥垂直于圆O所在的平面,∠ABC=60°.分析 由题意可得四边形ABCD是等腰梯形形,四边形ADCO,DOBC都是以半径为边长的菱形,
(Ⅰ)连接BD交OC于H,则H是BD中点,连接FH,即FH∥PB,可得PB∥平面COF
(Ⅱ)由四边形ADCO是以半径为边长的菱形,可得AC⊥CO,及PO⊥AC,可得AC⊥面POD,即可证AC⊥PD
解答 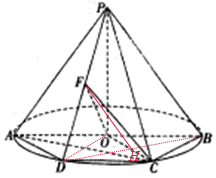 解:如图所示,∵AB是圆O的直径,∴△ABC是直角△,又,∠ABC=60°.
解:如图所示,∵AB是圆O的直径,∴△ABC是直角△,又,∠ABC=60°.
∴BC=$\frac{1}{2}AB$,又∵四边形ABCD是圆的内接四边形,∴四边形ABCD是等腰梯形形,
∴四边形ADCO,DOBC都是以半径为边长的菱形,
(Ⅰ)连接BD交OC于H,则H是BD中点,连接FH,
因为F为PD中点,∴FH∥PB,且PB?面COF,FH?平面COF
∴PB∥平面COF
(Ⅱ)∵四边形ADCO是以半径为边长的菱形
∴AC⊥CO,
∵PO⊥垂直于圆O所在的平面,∴PO⊥AC,且DO∩PO=O
∴AC⊥面POD,
∵PD?面POD,∴AC⊥PD
点评 考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力 空间想象能力,考查化归与转化思想、数形结合思想,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
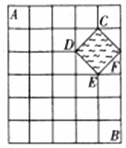 如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 6π | C. | 4π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com