Question

16．把正方形ABCD沿对角线BD折成直二面角，对于下列结论：
①AC⊥BD；②△ADC是正三角形；③AB与CD成60°角；④AB与平面BCD成60°角．
则其中正确结论的个数是（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 取BD的中点E，则AE⊥BD，CE⊥BD．根据线面垂直的判定及性质可判断①的真假；求出AC长后，可以判断②的真假；求出AB与平面BCD所成的角可判断③的真假；建立空间坐标系，利用向量法，求出AB与CD所成的角，可以判断④的真假；进而得到答案

解答 解：取BD的中点E，则AE⊥BD，CE⊥BD．
∴BD⊥面AEC．?
∴BD⊥AC，故①正确．?
设正方形边长为a，则AD=DC=a，AE=$\frac{\sqrt{2}}{2}$a=EC．
∴AC=a．?
∴△ADC为等边三角形，故②正确．?
∠ABD为AB与面BCD所成的角为45°，?
以E为坐标原点，EC、ED、EA分别为x，y，z轴建立直角坐标系，?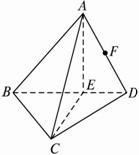
则A（0，0，$\frac{\sqrt{2}}{2}$a），B（0，-$\frac{\sqrt{2}}{2}$a，0），D（0，$\frac{\sqrt{2}}{2}$a，0），
C（$\frac{\sqrt{2}}{2}$a，0，0）．
$\overrightarrow{AB}$=（0，-$\frac{\sqrt{2}}{2}$a，-$\frac{\sqrt{2}}{2}$a），$\overrightarrow{DC}$=（$\frac{\sqrt{2}}{2}$a，-$\frac{\sqrt{2}}{2}$a，0）．
cos＜$\overrightarrow{AB}$，$\overrightarrow{DC}$＞=$\frac{1}{2}$，
∴＜$\overrightarrow{AB}$，$\overrightarrow{DC}$＞=60°，故③正确．
∠ABD为AB与面BCD所成的角为45°，故④不正确．?
故选：C

点评 本题考查的知识点是线面垂直的判定与性质，空间两点距离，线面夹角，异面直线的夹角，其中根据已知条件将正方形ABCD沿对角线BD折成直二面角A-BD-C，结合立体几何求出相关直线与直线、直线与平面的夹角，及线段的长是关键，是中档题．