
分析 对|$\overrightarrow{a}$|=|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2两边平方得出|$\overrightarrow{b}$|与向量夹角θ的关系,用θ表示出|$\overrightarrow{b}$|和|$\overrightarrow{a}+\overrightarrow{b}$|,利用三角函数的性质得出答案.
解答 解:∵|$\overrightarrow{a}$|=|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2,
∴${\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}=4$,
∴${\overrightarrow{b}}^{2}$=-$\overrightarrow{a}•\overrightarrow{b}$.
设$\overrightarrow{a},\overrightarrow{b}$夹角为θ,则$|\overrightarrow{b}|$=-2cosθ.$\frac{π}{2}<θ≤π$.
∴|$\overrightarrow{a}+\overrightarrow{b}$|2=${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$=4+$\overrightarrow{a}•\overrightarrow{b}$=4-4cos2θ=4sin2θ.
∴|$\overrightarrow{a}+\overrightarrow{b}$|=2sinθ,
∴|$\overrightarrow{b}$|+|$\overrightarrow{a}$+$\overrightarrow{b}$|=2sinθ-2cosθ=2$\sqrt{2}$sin($θ-\frac{π}{4}$).
∴当$θ-\frac{π}{4}$=$\frac{π}{2}$即$θ=\frac{3π}{4}$时,|$\overrightarrow{b}$|+|$\overrightarrow{a}$+$\overrightarrow{b}$|取得最大值2$\sqrt{2}$.
故答案为2$\sqrt{2}$.
点评 本题考查了平面向量的数量积运算,三角函数的图象与性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(m+1)≥0 | B. | f(m+1)≤0 | C. | f(m+1)>0 | D. | f(m+1)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
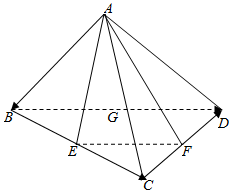 如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:
如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | [-3,3] | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com