
分析 (1)求出函数F(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可;
(2)问题转化为任意x1,x2∈[-1,+∞)且x1>x2有mf(x1)-g(x1)>mf(x2)-g(x2)>0恒成立,令h(x)=mf(x)-g(x)=mxex-$\frac{1}{2}$x2-x,x∈[-1,+∞),根据函数的单调性求出m的范围即可.
解答 解:(1)F(x)=f(x)+g(x)=xex+$\frac{1}{2}$x2+x,
F′(x)=(x+1)(ex+1),
令F′(x)>0,解得:x>-1,令F′(x)<0,解得:x<-1,
故F(x)在(-∞,-1)递减,在(-1,+∞)递增,
故F(x)min=F(-1)=-1-$\frac{1}{e}$;
(2)若任意x1,x2∈[-1,+∞)且x1>x2有m[f(x1)-f(x2)]>g(x1)-g(x2)恒成立,
则任意x1,x2∈[-1,+∞)且x1>x2有mf(x1)-g(x1)>mf(x2)-g(x2)>0恒成立,
令h(x)=mf(x)-g(x)=mxex-$\frac{1}{2}$x2-x,x∈[-1,+∞),
即只需h(x)在[-1,+∞)递增即可;
故h′(x)=(x+1)(mex-1)≥0在[-1,+∞)恒成立,
故m≥$\frac{1}{{e}^{x}}$,而$\frac{1}{{e}^{x}}$≤e,
故m≥e.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道综合题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
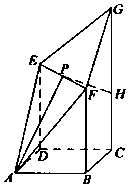 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
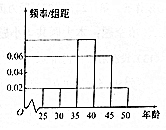 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 14 | 22 |
| 合计 | 24 | 18 | 42 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 9 | C. | 27 | D. | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
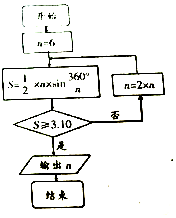 如图是利用我国古代数学家刘徽的割圆术设计的程序框图,则输出的n值为( )
如图是利用我国古代数学家刘徽的割圆术设计的程序框图,则输出的n值为( )| A. | 12 | B. | 24 | C. | 48 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,0),(5,0) | B. | (0,-5),(0,5) | C. | $(-\sqrt{29},0)$,$(\sqrt{29},0)$ | D. | $(0,-\sqrt{29})$,$(0,\sqrt{29})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com