
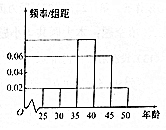
 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 14 | 22 |
| 合计 | 24 | 18 | 42 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)利用频率与频数的关系求出样本容量N、计算出a、b的值;
(2)求出年龄低于40岁的员工数,利用分层抽样原理求出每组抽取的人数;
(3)根据表中数据计算K2的观测值,查表得出概率结论.
解答 解:(1)总人数:N=$\frac{28}{5×0.02}$280,a=28;
第3组的频率是:1-5×(0.02+0.02+0.06+0.02)=0.4
所以b=280×0.4=112; …(3分)
(2)因为年龄低于40岁的员工在第1,2,3组,共有28+28+112=168(人),
利用分层抽样在168人中抽取42人,每组抽取的人数分别为:
第1组抽取的人数为28×$\frac{42}{168}$=7(人),第2组抽取的人数为28×$\frac{42}{168}$=7(人),
第3组抽取的人数为112×$\frac{42}{168}$=28(人),
所以第1,2,3组分别抽7人、7人、28人.…(6分)
(3)假设H0:“是否喜欢看国学类书籍和性别无关系”,根据表中数据,
求得K2的观测值k=$\frac{42{×(16×14-4×8)}^{2}}{24×18×20×22}$≈8.145>7.879,…(10分)
查表得P(K2≥7.879)=0.005,从而能在犯错误的概率不超过0.5%的前提下,
认为该单位的员工“是否喜欢看国学类书籍和性别有关系”.…(12分)
点评 本题考查了频率分布直方图与独立性检验的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -110 | B. | -220 | C. | 220 | D. | 110 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 0或-1 | D. | 0或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-12] | B. | (-∞,14] | C. | (-∞,-8] | D. | (-∞,$\frac{31}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥β,α∥β,则a∥α | B. | 若α∥β,a?α,则a∥β | ||
| C. | 若α∥β,a?α,b?β,则a∥b | D. | 若a∥β,b∥α,α∥β,则a∥b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com