
分析 (1)根据函数f(x)有意义,可得$\left\{\begin{array}{l}\frac{2-x}{3+x}≥0\\{3^x}-\frac{1}{3}>0\end{array}\right.$,解出x的范围可得定义域M.
(2)讲g(x)化简,转化为二次函数的问题,利用x∈M时,考查单调性可得值域.
解答 解:(1)由已知可得$\left\{\begin{array}{l}\frac{2-x}{3+x}≥0\\{3^x}-\frac{1}{3}>0\end{array}\right.⇒\left\{\begin{array}{l}-3<x≤2\\ x>-1\end{array}\right.$,
∴-1<x≤2,
所以M=(-1,2].
(2)由$g(x)={4^{x+\frac{1}{2}}}-{2^{x+2}}+1=2•{2^{2x}}+4•{2^x}+1=2{({{2^x}-1})^2}-1$,
∵x∈M,即-1<x≤2,
∴$\frac{1}{2}<{2^x}<4$,
∴当2x=1,即x=0时,g(x)min=-1,
当2x=4,即x=2时,g(x)max=17,
故得g(x)的值域为[-1,17].
点评 本题考查定义域的求法和指数函数的化简能力,转化思想,利用二次函数和指数的性质的单调性求解值域,属于函数函数性质应用题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于y=x轴对称 | D. | 关于原点轴对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
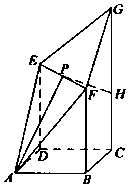 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
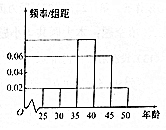 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 14 | 22 |
| 合计 | 24 | 18 | 42 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com