
(12分) 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且MD=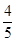 PD.
PD.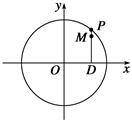
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为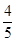 的直线被C所截线段的长度.
的直线被C所截线段的长度.
(1)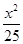 +
+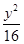 =1.(2)AB=
=1.(2)AB=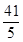 .
.
解析试题分析:设M的坐标为(x,y),P的坐标为(xP,yP),然后利用MD=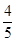 PD,把P点坐标用M点的坐标表示出来,代入圆的方程即可得到动点M的轨迹方程.
PD,把P点坐标用M点的坐标表示出来,代入圆的方程即可得到动点M的轨迹方程.
(1)设M的坐标为(x,y),P的坐标为(xP,yP),
由已知得 ∵P在圆上,
∵P在圆上,
∴x2+(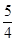 y)2=25,
y)2=25,
即轨迹C的方程为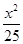 +
+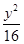 =1.
=1.
(2)过点(3,0)且斜率为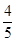 的直线方程为y=
的直线方程为y=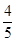 (x-3),
(x-3),
设直线与C的交点为A(x1,y1),B(x2,y2),将直线方程y=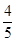 (x-3)代入C的方程,
(x-3)代入C的方程,
得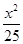 +
+ =1,即x2-3x-8=0.
=1,即x2-3x-8=0.
∴x1=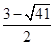 ,x2=
,x2=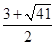 .
.
∴线段AB的长度为
AB=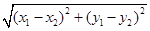
=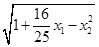
=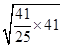 =
=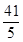 .
.
考点:求轨迹方程,圆和椭圆的方程,直线与椭圆的位置关系,两曲线的交点.
点评:本小题属于相关点法求轨迹方程要把主动点的坐标用被动点的坐标表示出来,然后再代入主动点所在曲线的方程即可求出动点的轨迹方程.在涉及直线与椭圆相交求弦长时要借助韦达定理及弦长公式,一般不考虑求交点坐标.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)已知椭圆C: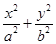 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+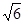 =0相切。
=0相切。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,椭圆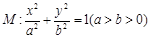 的离心率为
的离心率为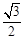 ,直线
,直线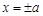 和
和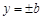 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.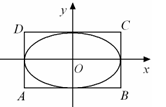
(Ⅰ)求椭圆M的标准方程;
(Ⅱ) 设直线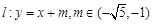 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点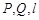 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点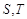 .求
.求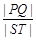 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0), 交椭圆于A、B两个不同点。
交椭圆于A、B两个不同点。
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆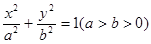 的离心率
的离心率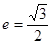 ,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且
,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且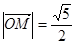 .
.
(1)求椭圆的方程;
(2)过(-1,0)的直线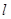 交椭圆于P,Q两点,求△POQ面积最大时直线
交椭圆于P,Q两点,求△POQ面积最大时直线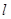 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知圆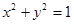 过椭圆
过椭圆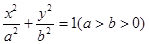 的两焦点,与椭圆有且仅有两个公共点;直线
的两焦点,与椭圆有且仅有两个公共点;直线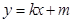 与圆
与圆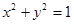 相切 ,与椭圆
相切 ,与椭圆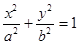 相交于
相交于 两点记
两点记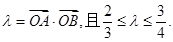
(1)求椭圆的方程;
(2)求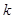 的取值范围;
的取值范围;
(3)求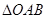 的面积S的取值范围.
的面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)
已知椭圆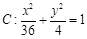 ,斜率为
,斜率为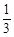 的直线
的直线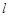 交椭圆
交椭圆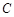 于
于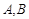 两点,且点
两点,且点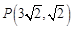 在直线
在直线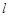 的上方,
的上方,
(1)求直线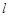 与
与 轴交点的横坐标
轴交点的横坐标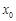 的取值范围;
的取值范围;
(2)证明: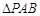 的内切圆的圆心在一条直线上.
的内切圆的圆心在一条直线上. 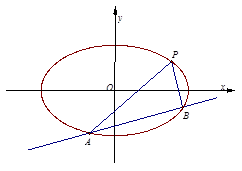
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com