
| A. | 1或$\frac{1}{2}$ | B. | $\frac{1}{2}$或2 | C. | 1或2 | D. | 1或3 |
分析 由已知可得分段函数f(x)的解析式,进而求出三个函数的极值点坐标,根据三点共线,则任取两点确定的直线斜率相等,可以构造关于c的方程,解方程可得答案.
解答 解:∵当2≤x≤4时,f(x)=1-(x-3)2,
当1≤x<2时,2≤2x<4,
则f(x)=$\frac{1}{c}$f(2x)=$\frac{1}{c}$[1-(2x-3)2],
此时当x=$\frac{3}{2}$时,函数取极大值$\frac{1}{c}$;
当2≤x≤4时,f(x)=1-(x-3)2,此时当x=3时,函数取极大值1,
当4<x≤8时,2<$\frac{1}{2}$x≤4
则f(x)=cf($\frac{1}{2}$x)=c(1-($\frac{1}{2}$x-3)2,
此时当x=6时,函数取极大值c,
∵函数的所有极大值点均落在同一条直线上,
即点($\frac{3}{2}$,$\frac{1}{c}$),(3,1),(6,c)共线,
∴$\frac{1-\frac{1}{c}}{3-\frac{3}{2}}$=$\frac{c-1}{6-3}$
解得c=1或2.
故选:C.
点评 本题考查的知识点是三点共线,函数的极值,其中根据已知分析出分段函数f(x)的解析式,进而求出三个函数的极值点坐标,是解答本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p是真命题 | B. | 命题p的否命题是假命题 | ||
| C. | 命题p的逆否命题是假命题 | D. | 命题p的否命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={(\sqrt{x+1})^2}$ | B. | $y=\root{3}{x^3}+1$ | C. | $y=\frac{x^2}{x}+1$ | D. | $y=\sqrt{x^2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
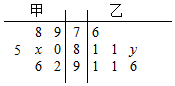 高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com