练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝sinx＋tanx.项数为27的等差数列{an}满足an∈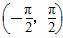，且公差d≠0.若f(a1)＋f(a2)＋…＋f(a27)＝0，则当k＝________时，f(ak)＝0.


    　14

    [解析]　∵f(x)＝sinx＋tanx为奇函数，且在x＝0处有定义，∴f(0)＝0.

    ∵{an}为等差数列且d≠0，

    ∴an(1≤n≤27，n∈N*)对称分布在原点及原点两侧，

    ∵f(a1)＋f(a2)＋…＋f(a27)＝0，∴f(a14)＝0.

    ∴k＝14.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，在△ABC中，AB＝5，BC＝3，CA＝4，且O是△ABC的外心，则＝(　　)

    A．6　　　　B．－6 　　　C．8　　　　D．－8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在数列{an}中，若a1＝1，an＋1＝2an＋3(n∈N*)，则数列{an}的通项an＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知{an}是等差数列，a1＋a2＝4，a7＋a8＝28，则该数列前10项和S10等于(　　)

    A．64  B．100  C．110  D．120

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}的前n项和为Sn，若M、N、P三点共线，O为坐标原点，且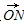＝a15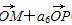 (直线MP不过点O)，则S20等于(　　)

    A．10  B．15  C．20  D．40

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}的前n项和为Sn，a5＝5，S5＝15，则数列的前100项和为(　　)

    A.  B.  C.  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如表定义函数f(x)：

    x

    1

    2

    3

    4

    5

    f(x)

    5

    4

    3

    1

    2

    对于数列{an}，a1＝4，an＝f(an－1)，n＝2,3,4，…，则a2014的值是(　　)

    A．1  B．2  C．3  D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有10个数，它们能构成一个以1为首项，－3为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    我们可以利用数列{an}的递推公式，求出这个数列各项的值，使得这个数列中的每一项都是奇数，则a24＋a25＝________；研究发现，该数列中的奇数都会重复出现，那么第8个5是该数列的第________项．

    查看答案和解析>>

    同步练习册答案