Question

3．如图，△P′AB是边长为$\sqrt{3}$+1的等边三角形，P′C=P′D=$\sqrt{3}$-1，现将△P′CD沿边CD折起至PCD将四棱锥P-ABCD，且PC⊥BD．
（Ⅰ）证明：BD⊥平面PAC；
（Ⅱ）求四棱锥P-ABCD的体积．

Answer 1

分析 （Ⅰ）根据正弦定理以及直线和平面垂直的判定定理即可证明BD⊥平面PAC；
（Ⅱ）求出四棱锥的高和底面积的大小，结合四棱锥的体积公式即可求四棱锥P-ABCD的体积．

解答 证明：（Ⅰ）连接AC交BD于O，
在△ABC中，BC=$\sqrt{3}+1-（\sqrt{3}-1）=2$，
则AC²=（$\sqrt{3}+1$）²+2²-2×$2（\sqrt{3}+1）×cos60°=6$，
即AC=$\sqrt{6}$，
由正弦定理得$\frac{2}{sin∠CAB}=\frac{\sqrt{6}}{sin60°}$，
即sin∠CAB=$\frac{2×\frac{\sqrt{3}}{2}}{\sqrt{6}}=\frac{\sqrt{2}}{2}$，
即∠CAB=45°，
同理得∠DBA=45°，
即∠AOB=90°，
即BD⊥AC，
∵PC⊥BD，且PC∩AC=C，
故BD⊥平面PAC；
（Ⅱ）取CD中点E，连接OE，PE，
∵PD=PC，∴CD⊥PE，
而AC=BD，AO=BO，
则OC=OD，
∴CD⊥OE，即CD⊥平面POE，
从而OP⊥CD，
由（Ⅰ）知，OP⊥BD，BD∩CD=D，
故OP⊥平面ABCD，
即棱锥P-ABCD的高为OP．
在直角三角形POC中，OP=$\sqrt{（\sqrt{3}-1）^{2}-（\sqrt{6}-\frac{\sqrt{6}+\sqrt{2}}{2}）^{2}}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$，
则${S}_{ABCD}=\frac{1}{2}|AC|•|BD|=\frac{1}{2}×\sqrt{6}×\sqrt{6}=3$，
则四棱锥P-ABCD的体积V=$\frac{1}{3}×3×\frac{\sqrt{6}-\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{2}$．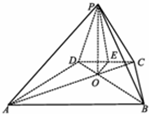

点评 本题主要考查空间四棱锥的体积的计算，以及空间直线和平面垂直的判断，考查学生的计算和推理能力．