练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知tan（π-a）=2，则
    1
    sinαcosα
    =（　　）
    A、
    5
    2
    B、
    7
    5
    C、-
    5
    2
    D、-
    7
    5
    考点：运用诱导公式化简求值,同角三角函数基本关系的运用
    专题：三角函数的求值
    分析：已知等式左边利用诱导公式化简求出tanα的值，原式利用同角三角函数间基本关系弦化切后将tanα的值代入计算即可求出值．
    解答： 解：∵tan（π-a）=-tanα=2，
    ∴tanα=-2，
    则原式=
    sin2α+cos2α
    sinαcosα
    =
    tan2α+1
    tanα
    =
    4+1
    -2
    =-
    5
    2
    ．
    故选：C．
    点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    “mn＜0”是方程mx2+ny2=1表示双曲线的（　　）条件．
    A、充分不必要B、必要不充分
    C、充要D、不充分不必要

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    =（2，-4），
    b
    =（3，4）则向量
    a
    在
    b
    方向上的投影为（　　）
    A、
    8
    		5
    5
    B、-
    8
    		5
    5
    C、2
    D、-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    等差数列{an}共有20项，其中奇数项的和为15，偶数项的和为45，则该数列的公差为（　　）
    A、-3B、3C、-2D、-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x∈（0，
    1
    4
    ），则y=x
    		1-4x
    的最大值为（　　）
    A、
    1
    6
    B、
    1
    4
    C、
    		3
    18
    D、
    		3
    9

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f（x）=ax+a+4，若f′（1）=2，则a等于（　　）
    A、1B、-2C、2D、-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆
    x2
    4
    +
    y2
    3
    =1，则以点M（-1，1）为中点的弦所在直线方程为（　　）
    A、3x-4y+7=0
    B、3x+4y-1=0
    C、4x-3y+7=0
    D、4x+3y+1=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}的前n项和为Sn=2n2，{bn}为等比数列，且a1=b1，b2（a2-a1）=b1．
    （1）求数列{an}和{bn}的通项公式；
    （2）设Cn=
    2
    an(4-log2bn)
    ，求数列{Cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

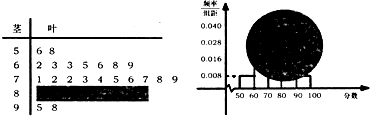    某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，可见部分如图（阴影部分为损坏数据）．据此解答如下问题：
    （Ⅰ）求本次测试成绩的中位数，并求频率分布直方图中[80，90）的矩形的高（用小数表示）；
    （Ⅱ）若要从分数在[80，100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90，100]之间的概率．

    查看答案和解析>>

    同步练习册答案