
| A. | $(0,\frac{{2-3\sqrt{2}}}{4})$ | B. | $[-\frac{9}{16},\frac{{2-3\sqrt{2}}}{4})$ | C. | $[\frac{{2-3\sqrt{2}}}{4},-\frac{1}{2})$ | D. | $[-\frac{9}{16},-\frac{1}{2})$ |
分析 先作出函数图象然后根据图象,根据f(x1)=f(x2),确定x1的取值范围然后再根据x1f(x2)-f(x2),转化为求在x1的取值范围即可.
解答 解:作出函数的图象:
∵存在x1,x2,当0≤x1<x2<2时,f(x1)=f(x2)
∴0≤x1<$\frac{1}{2}$,
∵x+$\frac{1}{2}$在[0,$\frac{1}{2}$)上的最小值为$\frac{1}{2}$;
2x-1在[$\frac{1}{2}$,2)的最小值为$\frac{\sqrt{2}}{2}$
∴x1+$\frac{1}{2}$≥$\frac{\sqrt{2}}{2}$,x1≥$\frac{\sqrt{2}-1}{2}$,
∴$\frac{\sqrt{2}-1}{2}$≤x1<$\frac{1}{2}$.
∵f(x1)=x1+$\frac{1}{2}$,f(x1)=f(x2)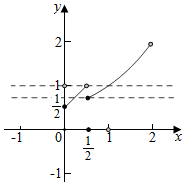
∴x1f(x2)-f(x2)=x1f(x1)-f(x1)2
=${x}_{1}^{2}+\frac{1}{2}{x}_{1}$-(x1+$\frac{1}{2}$)=x12-$\frac{1}{2}$x1-$\frac{1}{2}$,
设y=x12-$\frac{1}{2}$x1-$\frac{1}{2}$=(x1-$\frac{1}{4}$)2-$\frac{9}{16}$,($\frac{\sqrt{2}-1}{2}$≤x1<$\frac{1}{2}$),
则对应抛物线的对称轴为x=$\frac{1}{4}$,
∴当x=$\frac{1}{4}$时,y=-$\frac{9}{16}$,
当x=$\frac{\sqrt{2}-1}{2}$时,y=$\frac{2-3\sqrt{2}}{4}$,
即x1f(x2)-f(x2)的取值范围为[-$\frac{9}{16}$,$\frac{2-3\sqrt{2}}{4}$).
故选:B.
点评 本题主要考查分段函数的应用,以及函数零点和方程之间的关系,利用二次函数的单调性是解决本题的关键,综合性强,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}+ln2$ | B. | $\frac{1}{2}-ln2$ | C. | -1+ln2 | D. | 1+ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
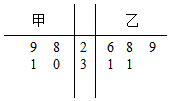 为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $S_{23}^{\;}$ | B. | S24 | C. | S25 | D. | S26 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com