
分析 求出函数的导数,求得切线的斜率,由直线的斜率公式,结合特殊角的正切公式即可得到所求角.
解答 解:$y=\sqrt{x}$的导数为y′=$\frac{1}{2\sqrt{x}}$,
可得曲线$y=\sqrt{x}$在$x=\frac{1}{4}$处的切线的斜率为k=$\frac{1}{2\sqrt{\frac{1}{4}}}$=1,
由斜率公式可得k=tanα=1,(0≤α<π,且α≠$\frac{π}{2}$),
解得倾斜角为$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,正确求导和运用直线的斜率公式是解题的关键,属于基础题.


科目:高中数学 来源: 题型:填空题
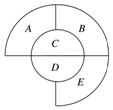 已知一个公园的形状如图所示,现有3种不同的植物要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的两块相邻区域种不同的植物,则不同的种法共有18种.
已知一个公园的形状如图所示,现有3种不同的植物要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的两块相邻区域种不同的植物,则不同的种法共有18种.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 256个 | B. | 18个 | C. | 16个 | D. | 10个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | -1 | 0 | 1 | 2 |
| P | a | b | c | $\frac{5}{18}$ |
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1),(0,+∞) | B. | (-∞,-1)∪(0,+∞) | C. | (-1,0) | D. | (-∞,0),(1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com