
分析 (1)把a=1代入,先对函数求导,然后求f(2),根据导数的几何意义可知,该点切线的斜率k=f′(2),从而求出切线方程.
(2)先对函数求导,分别解f′(x)>0,f′(x)<0,解得函数的单调区间,根据函数的单调性求函数的极值.
解答 解:(1)当a=1时,f(x)=$\frac{2x}{{x}^{2}+1}$,f(2)=$\frac{4}{5}$,
又f′(x)=$\frac{2(1+x)(1-x)}{{{(x}^{2}+1)}^{2}}$,f′(2)=-$\frac{6}{25}$,
所以,曲线y=f(x)在点(2,f(2))处的切线方程为y-$\frac{4}{5}$=-$\frac{6}{25}$(x-2),
即6x+25y-32=0.
(2)f′(x)=$\frac{-2(x-a)(ax+1)}{{{(x}^{2}+1)}^{2}}$,
由于a≠0,以下分两种情况讨论.
①当a>0时,令f'(x)=0,得到x1=-$\frac{1}{a}$,x2=a,
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,-$\frac{1}{a}$) | -$\frac{1}{a}$ | (-$\frac{1}{a}$,a) | a | (a,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
| x | (-∞,a) | a | (a,-$\frac{1}{a}$) | -$\frac{1}{a}$ | (-$\frac{1}{a}$,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
点评 本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
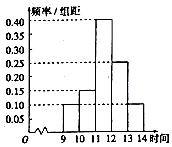 一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )| A. | 100万元 | B. | 10万元 | C. | 7.5万元 | D. | 6.25万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com