
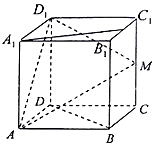
 如图边长为2的正方体ABCD-A1B1C1D1中,M、N分别是CC1,B1C1的中点.
如图边长为2的正方体ABCD-A1B1C1D1中,M、N分别是CC1,B1C1的中点.分析 (1)建立坐标系,求出平面AD1M的法向量$\overrightarrow{n}$和$\overrightarrow{{A}_{1}N}$的坐标,通过证明$\overrightarrow{n}⊥\overrightarrow{{A}_{1}N}$即可得出结论;
(2)计算两个半平面的法向量的夹角,得出结论.
解答 证明:(1)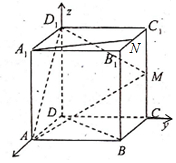 以D为原点,以DA,DC,DD1为轴建立空间坐标系,
以D为原点,以DA,DC,DD1为轴建立空间坐标系,
则A1(2,0,2),N(1,2,2,),M(0,2,1),A(2,0,0),D1(0,0,2),
∴$\overrightarrow{{A}_{1}N}$=(-1,2,0),$\overrightarrow{AM}$=(-2,2,1),$\overrightarrow{A{D}_{1}}$=(-2,0,2),
设平面AMD1的法向量为$\overrightarrow{n}$(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AM}=0}\\{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-2x+2y+z=0}\\{-2x+2z=0}\end{array}\right.$,令x=1得$\overrightarrow{n}$=(1,$\frac{1}{2}$,1),
∴$\overrightarrow{{A}_{1}N}•\overrightarrow{n}$=-1+1+0=0,∴$\overrightarrow{{A}_{1}N}⊥\overrightarrow{n}$,
又A1N?平面AMD1,
∴A1N∥平面AMD1.
(2)∵DC⊥平面ADD1,
∴$\overrightarrow{m}$=(0,1,0)是平面ADD1的一个法向量,
cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\frac{1}{2}}{1×\frac{3}{2}}$=$\frac{1}{3}$,
∴二面角M-AD1-D的余弦值为$\frac{1}{3}$.
点评 本题考查了线面平行的判定,空间向量与空间角的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 虚数 | B. | 纯虚数 | C. | 实数 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k+1 | B. | 2k+2 | C. | (2k+1)+(2k+2) | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国古代数学名著《九章算术》中记载了公元前344年商鞅造的一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取为3,其体积为12.6(立方升),则三视图中x的为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅造的一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取为3,其体积为12.6(立方升),则三视图中x的为( )| A. | 3.4 | B. | 4.0 | C. | 3.8 | D. | 3.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com