
分析 根据平面向量数量积的坐标运算求出f(x),利用三角恒等变换化f(x)为正弦型函数,由此求出f(x)的单调递增区间.
解答 解:∵$\overrightarrow{OA}$=(2sinx,cosx),$\overrightarrow{OB}$=(sinx,-2$\sqrt{3}$sinx),
∴f(x)=$\overrightarrow{OA}$$•\overrightarrow{OB}$+m+1
=2sin2x-2$\sqrt{3}$sinxcosx
=2•$\frac{1-cos2x}{2}$-$\sqrt{3}$sin2x+m+1
=-cos2x-$\sqrt{3}$sin2x+m+2
=-2($\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$sin2x)+m+2
=-2sin(2x+$\frac{π}{6}$)+m+2,
令$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,k∈Z,
∴$\frac{π}{3}$+2kπ≤2x≤$\frac{4π}{3}$+2kπ,k∈Z,
解得$\frac{π}{6}$+kπ≤x≤$\frac{2π}{3}$+kπ,k∈Z,
∴函数y=f(x)的单调递增区间是[$\frac{π}{6}$+kπ,$\frac{2π}{3}$+kπ],k∈Z.
点评 本题考查了平面向量数量积的坐标运算以及三角恒等变换问题,也考查了三角函数的单调性问题,是中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{17}}}{17}$ | B. | $\frac{{3\sqrt{2}}}{5}$ | C. | $\frac{{3\sqrt{17}}}{34}$ | D. | $\frac{{2\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
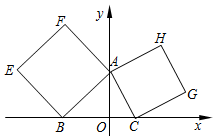 在平面直角坐标系xOy中,已知点A(0,2),B(-2,0),C(1,0),分别以△ABC的边AB、AC向外作正方形ABEF与ACGH,
在平面直角坐标系xOy中,已知点A(0,2),B(-2,0),C(1,0),分别以△ABC的边AB、AC向外作正方形ABEF与ACGH,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
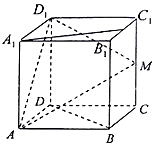 如图边长为2的正方体ABCD-A1B1C1D1中,M、N分别是CC1,B1C1的中点.
如图边长为2的正方体ABCD-A1B1C1D1中,M、N分别是CC1,B1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com