
分析 (Ⅰ)求出当a=1时,f(x)=$\frac{1}{x}$-1+lnx,x>0的导数,求得单调区间和极值、最值;
(Ⅱ)若函数f(x)在[1,+∞)上为增函数,即有f′(x)≥0在[1,+∞)恒成立.由参数分离和函数的最值求法,即可得到a的范围;
(Ⅲ)设an=(1+$\frac{1}{n}$)n,bn=(1+$\frac{1}{n}$)n+1,由$\underset{lim}{x→∞}(1+\frac{1}{x})^{x}$=e,得$\underset{lim}{n→∞}{a}_{n}=e$,$\underset{lim}{n→∞}{b}_{n}=e$,证明数列{an}的单调递增;数列{bn}的单调递减,即可判断大小.
解答 解:(Ⅰ)当a=1时,f(x)=$\frac{1}{x}$-1+lnx,x>0
f′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,
当x>1时,f′(x)>0,f(x)递增,当0<x<1时,f′(x)<0,f(x)递减.
即有x=1处f(x)取得极小值,也为最小值,且为0;
(Ⅱ)若函数f(x)在[1,+∞)上为增函数,即有f′(x)≥0在[1,+∞)恒成立.
即为$\frac{1}{x}$-$\frac{1}{a{x}^{2}}$≥0在[1,+∞)恒成立.即有$\frac{1}{a}$≤x在[1,+∞)恒成立.
而x≥1,即为$\frac{1}{a}$≤1,
解得a<0或a≥1;
(Ⅲ)设an=(1+$\frac{1}{n}$)n,bn=(1+$\frac{1}{n}$)n+1,
由$\underset{lim}{x→∞}(1+\frac{1}{x})^{x}$=e,得$\underset{lim}{n→∞}{a}_{n}=e$,$\underset{lim}{n→∞}{b}_{n}=e$,
由an=(1+$\frac{1}{n}$)n<($\frac{(1+\frac{1}{n})+(1+\frac{1}{n})+…+(1+\frac{1}{n})}{n+1}$)n+1=($\frac{n+2}{n+1}$)n+1=an+1,
故数列{an}的单调递增;
又bn=(1+$\frac{1}{n}$)n+1=$\frac{1}{(\frac{n}{n+1})^{n+1}}$=$\frac{1}{(1-\frac{1}{n+1})^{n+1}}$(令t=-(n+1))
=(1+$\frac{1}{t}$)t=at,
由at是关于t的增函数,而t是关于n的减函数,
由复合函数的单调性可得,
(1+$\frac{1}{n}$)n<e<(1+$\frac{1}{n}$)n+1.
故($\frac{n+1}{n}$)n+1(n∈N*)>e.
点评 本题考查导数的运用:求单调区间和极值、最值,同时考查不等式恒成立问题转化为求函数的最值,考查数列的单调性和运用,运用重要极限是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
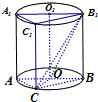 如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P
如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
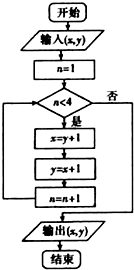
| A. | (11,12) | B. | (12,13) | C. | (13,14) | D. | (13,12) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com