练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知向量$\overrightarrow{a}=（{e}^{x}，1）$，向量$\overrightarrow{b}=（1，x-1）$，设函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$，则函数f（x）的零点个数为（　　）
    A．1 个B．2 个C．3 个D．4 个

    分析 由数量积得到函数f（x），求导判断其单调性，再由f（0）=0得答案．

    解答 解：由向量$\overrightarrow{a}=（{e}^{x}，1）$，向量$\overrightarrow{b}=（1，x-1）$，
    得f（x）=$\overrightarrow{a}•\overrightarrow{b}$=ex+x-1，
    ∵f′（x）=ex+1＞0，∴f（x）为实数集上的增函数，
    又f（0）=e0+0-1=0，
    ∴函数f（x）的零点个数为1个．
    故选：A．

    点评 本题考查平面向量的数量积运算，考查了函数零点的判断，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．已知命题p：?x∈R，x-2＞0，命题q：?x∈R，2x＞x2，则下列说法中正确的是（　　）
    A．命题p∨q是假命题B．命题p∧q是真命题
    C．命题p∧（￢q）是真命题D．命题p∨（￢q）是假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知复数z=$\frac{-1-2i}{{{{（1+i）}^2}}}$，则$\overline z$=（　　）
    A．-$\frac{3}{4}+\frac{1}{4}$iB．-$\frac{1}{4}+\frac{3}{4}$iC．-1+$\frac{1}{2}$iD．-1-$\frac{1}{2}$i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知x，y满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-2y+4≥0}\\{3x-y-3≤0}\end{array}\right.$，则|x+y+1|的最大值为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=$\frac{1-x}{ax}$+lnx
    （Ⅰ）当a=1时，求函数f（x）的最小值；
    （Ⅱ）若函数f（x）在[1，+∞）上为增函数，求实数a的取值范围；
    （Ⅲ）试比较（$\frac{n+1}{n}$）n+1（n∈N*）与e（e为自然对数的底数）的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在复平面上，复数z=a+bi（a，b∈R）与复数i（i-2）关于实轴对称，则a+b的值为（　　）
    A．1B．-3C．3D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知命题p：?x∈R，ex＞0命题q：?x∈R，x-2＞x2，则（　　）
    A．命题p∨q是假命题B．命题p∧q是真命题
    C．命题p∧（?q）是真命题D．命题p∨（?q）是假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

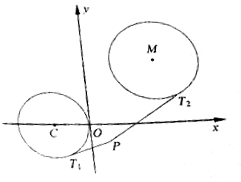    16．设圆C：（x+4）2+y2=16，动圆M：x2+y2-2ax-2（8-a）y+4a+22=0，平面内是还有存在定点P，过点P作圆C的一条切线，切点为T1，过点P作圆M的一条切线，切点为T2，使无穷多个圆M，满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$？如果存在，求出所有这样的点P；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．下列四个命题中真命题的个数是（　　）
    ①“x=1”是“x2-3x+2=0”的充分不必要条件
    ②命题“?x∈R，sinx≤1”的否定是“?x∈R，sinx＞1”
    ③命题p：?x∈[1，+∞），lgx≥0，命题q：?x∈R，x2+x+1＜0，则p∨q为真命题．
    A．0B．1C．2D．3

    查看答案和解析>>

    同步练习册答案