
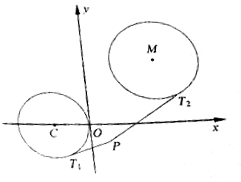
 设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.
设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由. 分析 设P(x,y),利用$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$,可得$\frac{(x+4)^{2}+{y}^{2}-16}{{x}^{2}+{y}^{2}-2ax-2(8-a)y+4a+22}$=$\frac{1}{4}$,从$\left\{\begin{array}{l}{2x-2y-4=0}\\{3{x}^{2}+3{y}^{2}+32x+16y-22=0}\end{array}\right.$,即可得出结论.
解答 解:圆C:(x+4)2+y2=16的圆心为(-4,0),半径为4,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0的圆心为(a,8-a),半径为$\sqrt{2{a}^{2}-20a+42}$
设P(x,y),则
因为$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$,
所以$\frac{(x+4)^{2}+{y}^{2}-16}{{x}^{2}+{y}^{2}-2ax-2(8-a)y+4a+22}$=$\frac{1}{4}$,
所以3x2+3y2+(32+2a)x+2(8-a)y-4a-22=0,
所以a(2x-2y-4)+(3x2+3y2+32x+16y-22)=0,
所以$\left\{\begin{array}{l}{2x-2y-4=0}\\{3{x}^{2}+3{y}^{2}+32x+16y-22=0}\end{array}\right.$,
可得y2+10y+9=0,∴y=-1或-9,
∴P(1,-1)或P(-7,-9).
点评 本题考查圆与圆的位置关系,考查学生的计算能力,属于中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,1] | C. | [-1,2] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k>-$\frac{b}{a}$ | B. | k<$\frac{b}{a}$ | C. | k>$\frac{b}{a}$或k<-$\frac{b}{a}$ | D. | -$\frac{b}{a}$<k<$\frac{b}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,5] | B. | [-2,2] | C. | [-2,5] | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com