
分析 由题意设出圆的方程,把点M的坐标代入圆的方程,结合圆心到直线的距离列式求解.
解答 解:由题意设圆的方程为(x-a)2+y2=r2(a>0),
由点M(0,$\sqrt{5}$)在圆上,且圆心到直线2x-y=0的距离为$\frac{4\sqrt{5}}{5}$,
得$\left\{\begin{array}{l}{{a}^{2}+5={r}^{2}}\\{\frac{|2a|}{\sqrt{5}}=\frac{4\sqrt{5}}{5}}\end{array}\right.$,解得a=2,r=3.
∴圆C的方程为:(x-2)2+y2=9.
故答案为:(x-2)2+y2=9.
点评 本题考查圆的标准方程,训练了点到直线的距离公式的应用,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
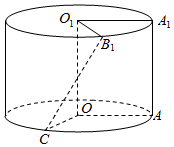 将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{2}{3}$π,$\widehat{A1B1}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{2}{3}$π,$\widehat{A1B1}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年龄x | 0.3 | 1.2 | 1.7 | 1.9 | 2.2 | 2.6 | 3.1 | 3.2 | 3.8 | 4.0 |
| 身高y | 63 | 71 | 76 | 79 | 83 | 87 | 91 | 93 | 97 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com