
| A. | ① | B. | ①② | C. | ①③ | D. | ①②③ |
分析 根据已知中M(x1,y1),N(x2,y2)两点之间的“直角距离”为|MN|=|x1-x2|+|y1-y2|,逐一分析给定三个结论的真假,可得答案.
解答 解:对于①到原点的“折线距离”等于1的点的集合{(x,y)||x|+|y|=1},
是一个正方形,面积为2,故①正确;
对于②设直线2x-y+3=0与x=1,y=1的交点分别为(1,5),(-1,1),
当B与(-1,1)重合时,|AB|的最小值为2,故②正确;
③O为坐标原点,M为曲线x${\;}^{\frac{1}{2}}$+y${\;}^{\frac{1}{2}}$=2上任意一点,
则当M坐标为(1,1)时,|OM|取最小值2.
当M坐标为(0,4),(4,0)时,|OM|取最大值4.
故真命题有:①②.
故选:B.
点评 本题主要考查了“折线距离”的定义,以及分析问题解决问题的能力,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
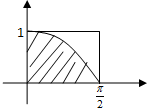

| A. | 60 | B. | 62 | C. | 64 | D. | 66 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 9 | C. | 12 | D. | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com