
| A�� | 30�� | B�� | 60�� | C�� | 30���150�� | D�� | 60���120�� |
���� �������|$\overrightarrow{b}$-t$\overrightarrow{a}$|��Ϊ$|\overrightarrow{a}|t$ �Ķ��κ����������СֵΪ$\sqrt{3}$���$\overrightarrow{a}$��$\overrightarrow{b}$�ļнǵ�����ֵ����𰸿���
��� �⣺��$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ�ȣ���|$\overrightarrow{b}$|=2��
��$|\overrightarrow{b}-t\overrightarrow{a}|=\sqrt{��\overrightarrow{b}-t\overrightarrow{a}��^{2}}=\sqrt{{\overrightarrow{b}}^{2}-2t\overrightarrow{a}•\overrightarrow{b}+{t}^{2}{\overrightarrow{a}}^{2}}$
=$\sqrt{{\overrightarrow{a}}^{2}{t}^{2}-4|\overrightarrow{a}|tcos��+4}$��
��$|\overrightarrow{a}|t=2cos��$ʱ����4cos2��-8cos2��+4=3��
��$cos��=��\frac{1}{2}$��
��$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ�ȵ�ȡֵ��Χ��[0����]��
���=60���120�㣮
��ѡ��D��
���� ���⿼��ƽ�����������������㣬���������������������ļнǣ����е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��c��b | B�� | b��a��c | C�� | a��b��c | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$+$\frac{1}{2}$i | B�� | -$\frac{1}{2}$-$\frac{1}{2}$i | C�� | $\frac{1}{2}$-$\frac{1}{2}$i | D�� | $\frac{1}{2}$+$\frac{1}{2}$i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪ABCD�Ǿ��Σ���PA=a��PA��ƽ��ABCD��M��N�ֱ���AB��PC���е㣮
��֪ABCD�Ǿ��Σ���PA=a��PA��ƽ��ABCD��M��N�ֱ���AB��PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
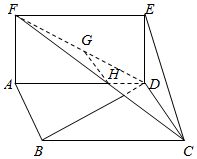 ��ͼ��ƽ���ı���ABCD�У�CD=1����BCD=60�㣬��BD��CD��������ADEF����ƽ���ƽ��ABCD��ֱ��G��H�ֱ���DF��FC���е㣮
��ͼ��ƽ���ı���ABCD�У�CD=1����BCD=60�㣬��BD��CD��������ADEF����ƽ���ƽ��ABCD��ֱ��G��H�ֱ���DF��FC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
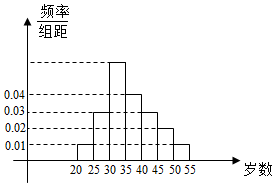 ij��ѧ������ĩ��֯��ְԱ��������һ���^��ɽ�����Ļ����N�˲μӣ��ֽ����вμ��߰����������Ϊ[20��25����[25��30����[30��35����[35��40����[40��45����[45��50����[50��55�������飬��Ƶ�ʷֲ�ֱ��ͼ������ʾ����֪[35��40������IJμ�����8�ˣ�
ij��ѧ������ĩ��֯��ְԱ��������һ���^��ɽ�����Ļ����N�˲μӣ��ֽ����вμ��߰����������Ϊ[20��25����[25��30����[30��35����[35��40����[40��45����[45��50����[50��55�������飬��Ƶ�ʷֲ�ֱ��ͼ������ʾ����֪[35��40������IJμ�����8�ˣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com