
| 4 |
| 3 |
| 2 |
| k |
| 4 |
| 3 |
| ∫ | 1 -
|
| ∫ | 1 -
|
| 1 |
| 2 |
| | | 1 -
|
| 343 |
| 54 |
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
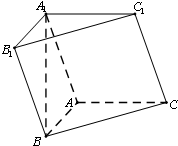 如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.
如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.| 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| z |
| 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
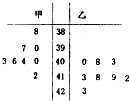 为调查甲乙两人网站受欢迎的程度,随机选取了某个月1号至8号,统计这8天内每天同一时间段的点击量,得到如图所示的茎叶图.
为调查甲乙两人网站受欢迎的程度,随机选取了某个月1号至8号,统计这8天内每天同一时间段的点击量,得到如图所示的茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:
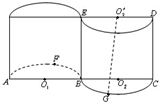 如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com