考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:求出方程
-=1表示双曲线的m的范围判断①;由双曲线的定义求出|PF
2|判断②;
由题意求出双曲线的离心率的范围判断③;联立直线与双曲线方程求解交点判断④.
解答:
解:对于①,当m>5时,
-=1表示双曲线,
若
-=1表示双曲线,则(5-m)(1-m)>0,解得m<1或m>5,
∴“m>5”是“
-=1表示双曲线”的充分不必要条件,命题①正确;
对于②,已知P为双曲线
-=1上一点,F
1,F
2分别为双曲线的左,右焦点,则|PF
1|-|PF
2|=±10,
若|PF
1|=11,则|PF
2|=21或1,命题②正确;
对于③,若在双曲线
-=1(a>0,b>0)右支上存在点P满足|PF
1|=3|PF
2|,
设P点的横坐标为x,∵|PF
1|=3|PF
2|,P在双曲线右支(x≥a),
根据双曲线的第二定义,可得3e(x-
)=e(x+
),∴ex=2a,
∵x≥a,∴ex≥ea,
∴2a≥ea,∴e≤2,
∵e>1,∴1<e≤2.
则双曲线的离心率的范围是(1,2],命题③正确;
对于④,联立
,得
,直线3x-4y-4=0与双曲线
-=1有一个交点,命题④错误.
∴正确的命题是①②③.
故答案为:①②③.
点评:本题考查了命题的真假判断与应用,考查了圆锥曲线的简单几何性质,考查了直线与圆锥曲线的关系问题,是中档题.



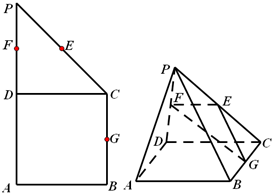 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.