
已知函数f(x)=xln x.
(1)求f(x)的单调区间和极值;
(2)设A(x1,f(x1)),B(x2,f(x2)),且x1≠x2,证明: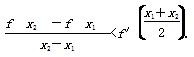
解:(1)f(x)的定义域为(0,+∞),
f′(x)=ln x+x· =1+ln x.
=1+ln x.
令f′(x)>0,则ln x>-1=ln 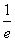 ,∴x>
,∴x>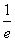 ;令f′(x)<0,则ln x<-1=ln
;令f′(x)<0,则ln x<-1=ln 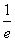 ,∴0<x<
,∴0<x<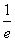 ,
,
∴f(x)的单调递增区间是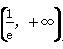 ,单调递减区间是
,单调递减区间是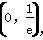 ,
,
f(x)极小值=f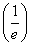 =
=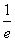 ln
ln 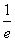 =-
=-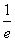 ,f(x)无极大值.
,f(x)无极大值.
(2)不防设x1<x2,
 =ln
=ln 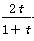 +
+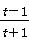
=ln 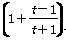 -
-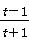 ,
,
令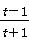 =x(x>0),h(x)=ln(1+x)-x,
=x(x>0),h(x)=ln(1+x)-x,
则h′(x)=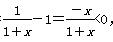 ,h(x)在(0,+∞)上单调递减,
,h(x)在(0,+∞)上单调递减,
∴h(x)<h(0)=0,
即ln (1+x)<x,即g′(t)=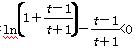 恒成立,
恒成立,
∴g(t)在(1,+∞)上是减函数,∴g(t)<g(1)=0,
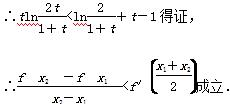


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
若函数f(x)=xcos x在(0,+∞)内的全部极值点按从小到大的顺序排列为a1,a2,…,an,…,则对任意正整数n必有( )
A.π<an+1-an<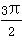 B.
B.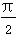 <an+1-an<π
<an+1-an<π
C.0<an+1-an<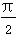 D.-
D.-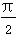 <an+1-an<0
<an+1-an<0
查看答案和解析>>
科目:高中数学 来源: 题型:
等差数列{an}中,如果a1+a4+a7=39,a3+a6+a9=27,则数列{an}前9项的和为( )
A.297 B.144
C.99 D.66
查看答案和解析>>
科目:高中数学 来源: 题型:
数列{an}的首项为3,{bn}为等差数列,且bn=an+1-an(n∈N*),若b3=-2,b10=12,则a8=( )
A.0 B.3
C.8 D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
下列5个命题中,正确命题的个数是( )
①对于命题p:∃x∈R,使得x2+x+1<0,则綈p:∀x∈R,均有x2+x+1>0;
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本的中心点为(4,5),则回归直线方程为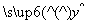 =1.23x+0.08;
=1.23x+0.08;
④若实数x,y∈[-1,1],则满足x2+y2≥1的概率为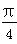 ;
;
⑤曲线y=x2与y=x所围成图形的面积是S= (x-x2)dx.
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com