
分析 (1)令t=cosθ∈[0,1],可得$g(t)=-{(t-\frac{{\sqrt{3}}}{2})^2}-2\sqrt{3}+\frac{7}{4}$,可得:g(t)在$[{0,\frac{{\sqrt{3}}}{2}}]$上单调递增,在$[{\frac{{\sqrt{3}}}{2},1}]$上单调递减,又t=cosθ在$[{0,\frac{π}{2}}]$上单调递减,令$\frac{{\sqrt{3}}}{2}≤t≤1$,即可解得函数f(x)的单调递增区间.
(2)由题意可得:$m>\frac{{2-{{cos}^2}θ}}{2-cosθ}=4-[(2-cosθ)+\frac{2}{2-cosθ}]$,由$θ∈[0,\frac{π}{2}]$,可得2-cosθ∈[1,2],利用基本不等式即可得解m的取值范围.
解答 解:(1)令t=cosθ∈[0,1],可得:$y=-{t^2}+\sqrt{3}t-2\sqrt{3}+1=-{({t-\frac{{\sqrt{3}}}{2}})^2}-2\sqrt{3}+\frac{7}{4}$,
记$g(t)=-{(t-\frac{{\sqrt{3}}}{2})^2}-2\sqrt{3}+\frac{7}{4}$,可得:g(t)在$[{0,\frac{{\sqrt{3}}}{2}}]$上单调递增,在$[{\frac{{\sqrt{3}}}{2},1}]$上单调递减.
又t=cosθ在$[{0,\frac{π}{2}}]$上单调递减.令$\frac{{\sqrt{3}}}{2}≤t≤1$,解得$0≤θ≤\frac{π}{6}$,
故函数f(x)的单调递增区间为$[{0,\frac{π}{6}}]$.…(6分)
(2)由g(θ)<-1得(2-cosθ)m>2-cos2θ,
即:$m>\frac{{2-{{cos}^2}θ}}{2-cosθ}=4-[(2-cosθ)+\frac{2}{2-cosθ}]$,
∵$θ∈[0,\frac{π}{2}]$,
∴2-cosθ∈[1,2],
∴$(2-cosθ)+\frac{2}{2-cosθ}≥2\sqrt{2}$,等号成立时cosθ=2-$\sqrt{2}$.
故:4-[(2-cosθ)+$\frac{2}{2-cosθ}$]的最大值是4-2$\sqrt{2}$.
从而m>4-2$\sqrt{2}$.…(12分)
点评 本题考查二次函数的图象和性质及恒成立问题,考查了基本不等式的应用,考查分类讨论思想,考查学生分析问题解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2或-3 | B. | 3或-2 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
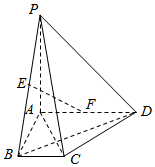 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,BC=1,AD=PA=$\sqrt{2}$AB=2,E,F分别为PB,AD的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,BC=1,AD=PA=$\sqrt{2}$AB=2,E,F分别为PB,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com