
 已知三棱柱ABC-A1B1C1中,A1A⊥底面ABC,∠BAC=90°,A1A=1,$AB=\sqrt{3}$,AC=2,E、F分别为棱C1C、BC的中点.
已知三棱柱ABC-A1B1C1中,A1A⊥底面ABC,∠BAC=90°,A1A=1,$AB=\sqrt{3}$,AC=2,E、F分别为棱C1C、BC的中点.分析 (I)由AC⊥AB,AC⊥AA1即可得出AC⊥平面ABB1A1,于是AC⊥A1B;
(II)以A为原点建立坐标系,求出$\overrightarrow{EF}$和 $\overrightarrow{{A}_{1}B}$的坐标,计算cos<$\overrightarrow{EF},\overrightarrow{{A}_{1}B}$>即可得出直线EF与A1B所成的角;
(III)求出$\overrightarrow{A{A}_{1}}$和平面EFG的法向量$\overrightarrow{n}$,则sin∠HA1A=|cos<$\overrightarrow{n}$,$\overrightarrow{A{A}_{1}}$>|.
解答 证明:(Ⅰ)∵AA1⊥底面ABC,AC?平面ABC
∴AC⊥AA1.
∵∠BAC=90°,∴AC⊥AB.
又A1A?平面AA1B1B,AB?平面AA1B1B,A1A∩AB=A,
∴AC⊥平面A1ABB1.
∵A1B?平面A1ABB1,
∴AC⊥A1B.
(Ⅱ)以A为原点建立空间直角坐标系A---xyz,如图所示:
则A1(0,0,1),$B({\sqrt{3},0,0})$,$E({0,2,\frac{1}{2}})$,$F({\frac{{\sqrt{3}}}{2},1,0})$.
∴$\overrightarrow{{A_1}B}=({\sqrt{3},0,-1})$,$\overrightarrow{EF}=({\frac{{\sqrt{3}}}{2},-1,-\frac{1}{2}})$.
∴$cos\left?{\overrightarrow{{A_1}B},\overrightarrow{EF}}\right>=\frac{{\overrightarrow{{A_1}B}•\overrightarrow{EF}}}{{|{\overrightarrow{{A_1}B}}|•|{\overrightarrow{EF}}|}}=\frac{{\sqrt{2}}}{2}$.
直线EF与A1B所成的角为45°.
(Ⅲ)$G({0,0,\frac{1}{2}})$,$\overrightarrow{GE}=({0,2,0})$,$\overrightarrow{GF}=({\frac{{\sqrt{3}}}{2},1,-\frac{1}{2}})$.$\overrightarrow{A{A}_{1}}$=(0,0,1).
设平面GEF的法向量为$\overrightarrow{n}$=(x,y,z),
则 $\left\{\begin{array}{l}\overrightarrow n⊥\overrightarrow{GE}\\ \overrightarrow n⊥\overrightarrow{GF}\end{array}\right.$,∴$\left\{\begin{array}{l}2y=0\\ \frac{{\sqrt{3}}}{2}x+y-\frac{1}{2}z=0.\end{array}\right.$
令$z=\sqrt{3}$,则$\overrightarrow n=({1,0,\sqrt{3}})$.
∴cos<$\overrightarrow{n},\overrightarrow{A{A}_{1}}$>=$\frac{\overrightarrow{n}•\overrightarrow{A{A}_{1}}}{|\overrightarrow{n}||\overrightarrow{A{A}_{1}}|}$=$\frac{\sqrt{3}}{2}$.
∵A1在平面EFG内的射影为H,∴∠HA1A位AA1与平面EFG所成的角,
∴sin∠HA1A=|cos<$\overrightarrow{n},\overrightarrow{A{A}_{1}}$>|=$\frac{\sqrt{3}}{2}$.
∴∠HA1A=$\frac{π}{3}$.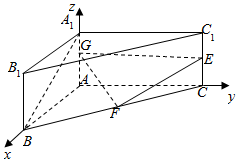
点评 本题考查了线面垂直的判定与性质,空间向量的应用与空间角的计算,属于中档题.


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:选择题
 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,则三棱锥P-ABC的正视图与俯视图的面积之比的最大值为( )
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,则三棱锥P-ABC的正视图与俯视图的面积之比的最大值为( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 选修4-1 | 选修4-4 | 选修4-5 | |
| 男生(人) | 10 | 6 | 4 |
| 女生(人) | 2 | 6 | 14 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
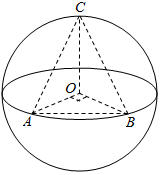 已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为$\frac{32}{3}$,则球O的表面积为64π.
已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为$\frac{32}{3}$,则球O的表面积为64π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0°,35°] | B. | (0°,90°] | C. | [35°,90°) | D. | [35°,90°] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-18,6] | B. | [6-5$\sqrt{2}$,6+5$\sqrt{2}$] | C. | [-16,4] | D. | [-6-5$\sqrt{2}$,-6+5$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com