
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 6个 |
分析 由题意,偶函数f(x)在区间[-3,3]上的值域为[-1,0],确定f(x)=0,即可得出y=f[f(x)]+1在区间[-3,3]上的零点个数.
解答 解:∵当x∈[-3,-2]时,f(x)=x2+4x+3=(x+2)2-1∈[-1,0];
又f(x)为R上的偶函数,
∴当x∈[2,3]时,f(x)∈[-1,0];
又f(x+2)=f(x),∴f(x)为以2为周期的函数,
由题意,偶函数f(x)在区间[-3,3]上的值域为[-1,0],
由f[f(x)]+1=0得到f[f(x)]=-1,于是可得f(x)=0或±2(舍弃),
由f(x)=0可得x=±1,±3,
所以y=f[f(x)]+1在区间[-3,3]上的零点个数为4.
故选:C,
点评 本题考查函数的周期性、奇偶性、函数图象的对称性,体现数形结合的数学思想.考查的知识点是根的存在性及根的个数判断,其中根据已知条件分析函数的性质,进而判断出函数零点的分布情况是解答本题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {-1,0,2} | C. | {-1,0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
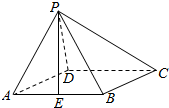 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$且0<f(1)<g(2) | B. | f(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$且0<f(1)<g(2) | ||
| C. | f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$且g(2)<f(1)<0 | D. | f(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$且g(2)<f(1)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 积极支持改革 | 不太支持改革 | 合 计 | |
| 工作积极 | 50 | 10 | 60 |
| 工作一般 | 10 | 10 | 20 |
| 合 计 | 60 | 20 | 80 |
| A. | 有99%的把握说事件A与B有关 | B. | 有95%的把握说事件A与B有关 | ||
| C. | 有90%的把握说事件A与B有关 | D. | 事件A与B无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=3x-1 | C. | y=log2(x+1) | D. | y=-sinx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com