练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．执行如图的程序框图，输出的S的值为（　　）
    A．6B．5C．4D．3

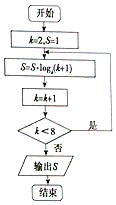
    分析 根据程序框图的功能是求S=1•log23•log34•log45•log56•log67•log78•log88，判断终止程序运行的k值，利用对数换底公式求得S值．

    解答 解：由程序框图得：第一次运行S=1•log23，k=3；
    第二次运行S=1•log23•log24，k=4；
    第二次运行S=1•log23•log34•log45，k=5；
    第三次运行S=1•log23•log34•log45•log56，k=6；
    …
    直到k=8时，程序运行终止，此时S=1•log23•log34•log45•log56•log67•log78•log88=3；
    故选：D．

    点评 本题考查了循环结构的程序框图，判断程序框图的运行功能是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．已知a=0.33，b=30.3，c=0.23，则a，b，c的大小关系为（　　）
    A．a＜b＜cB．c＜a＜bC．b＜a＜cD．c＜b＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在△ABC中，角A、B、C所对的边分别为a，b，c，$\sqrt{3}$bcosA=asinB．
    （1）求A；
    （2）若a=$\sqrt{2}$，$\frac{c}{a}$=$\frac{sinA}{sinB}$，求△ABC的周长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

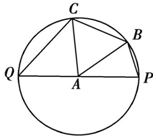    16．已知PQ是半径为1的圆A的直径，B，C为不同于P，Q的两点，如图所示，记∠PAB=θ．
    （1）若BC=$\sqrt{2}$，求四边形PBCQ的面积的最大值；
    （2）若BC=1，求$\overrightarrow{BP}$•$\overrightarrow{CQ}$的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知数列{an}为等比数列，则下列结论正确的是（　　）
    A．a1+a3≥2a2B．若a3＞a1，则a4＞a2C．若a1=a3，则a1=a2D．a12+a32≥2a22

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．函数f（x）=x1nx-ax2-x（a∈R）．
    （I）若函数f（x）在x=1处取得极值，求a的值；
    （II）若函数f（x）的图象在直线y=-x图象的下方，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知函数y=f（x）（x∈R）满足f（x+1）=-f（x），且当x∈（-1，1]时，f（x）=|x|，函数g（x）=$\left\{\begin{array}{l}sinπx，x＞0\\-\frac{1}{x}，x＜0\end{array}$，则函数h（x）=f（x）-g（x）在区间[-5，5]上的零点的个数为（　　）
    A．8B．9C．10D．11

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知数列{an}的前n项和为Sn，且Sn=2n+1-2（n∈N*）．
    （Ⅰ） 求数列{an}的通项公式；
    （Ⅱ） 令bn=nan，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若变量x，y满足约束条件$\left\{\begin{array}{l}{y≤4}\\{x+y-4≥0}\\{x-y≥0}\end{array}\right.$，则z=2x+y的最小值是（　　）
    A．4B．6C．8D．12

    查看答案和解析>>

    同步练习册答案