
分析 利用正弦函数的图象与性质进行判断,
解答 解:f($\frac{2015π}{3}$)=|cos$\frac{2015π}{3}$|sin$\frac{2015π}{3}$=|cos(672π-$\frac{π}{3}$)|sin(672π-$\frac{π}{3}$)=cos$\frac{π}{3}$sin(-$\frac{π}{3}$)=$\frac{1}{2}×$(-$\frac{\sqrt{3}}{2}$)=-$\frac{\sqrt{3}}{4}$.故①正确;
|f(x)|的图象是轴对称图形,当x1,x2关于|f(x)|的对称轴对称时,显然x1≠x2+kπ(k∈Z).故②错误;
当x∈$[-\frac{π}{4},\frac{π}{4}]$时,cosx>0,∴f(x)=cosxsinx=$\frac{1}{2}$sin2x,此时2x∈[-$\frac{π}{2}$,$\frac{π}{2}$],∴f(x)在区间$[-\frac{π}{4},\frac{π}{4}]$上单调递增;故③正确;
∵f(-$\frac{π}{4}$)=-$\frac{1}{2}$,f($\frac{3π}{4}$)=$\frac{1}{2}$,∴函数f(x)的最小正周期不是π.故④错误;
∵|cosx|≥0,∴f(x)的对称中心就是y=sinx的对称中心,故⑤正确;
故答案为:①③⑤.
点评 本题考查了三角函数的图象与性质,三角函数的周期及单调性判断,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值-1 | B. | 最大值14 | C. | 最大值9 | D. | 最大值4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{3}$ | B. | -2 | C. | $\frac{2}{3}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤3} | B. | {x|-2≤x≤3} | C. | {x|1<x≤3} | D. | {x|-2≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | (x-1)2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{2}+{y^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
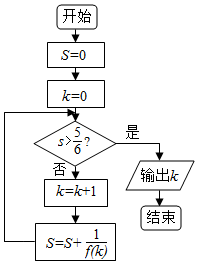
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com