
| A. | {x|-2<x≤3} | B. | {x|-2≤x≤3} | C. | {x|x<-2或x>3} | D. | {x|-2<x<3} |
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
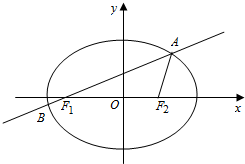 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α内所有的直线都与a异面 | B. | α内不存在与a平行的直线 | ||
| C. | α内所有的直线都与a相交 | D. | 直线a与平面α有公共点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC是边长为2的正三角形,AE⊥平面ABC,且AE=1,又平面BCD⊥平面ABC,且BD=CD,BD⊥CD.
如图,△ABC是边长为2的正三角形,AE⊥平面ABC,且AE=1,又平面BCD⊥平面ABC,且BD=CD,BD⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| A. | 210 | B. | 211.5 | C. | 212 | D. | 212.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4} | B. | {3,4,7} | C. | {3,7} | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com