
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中选择两个,补充在下面问题中,并给出解答.已知数列
这三个条件中选择两个,补充在下面问题中,并给出解答.已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足________,________;又知正项等差数列
,满足________,________;又知正项等差数列![]() 满足
满足![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)证明:![]() .
.
【答案】(1)选法见解析,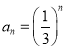 ,
,![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)若选择①②
先由![]() ,当
,当![]() ≥2时,
≥2时,![]() ,两式相减整理得
,两式相减整理得![]() ,再求出
,再求出![]() ,进而说明数列
,进而说明数列![]() 是等比数列,求出
是等比数列,求出![]() ,设正项等差数列
,设正项等差数列![]() 的公差为
的公差为![]() ,由已知条件求出
,由已知条件求出![]() ,进而求得
,进而求得![]() ;
;
若选择②③
先由![]() ,当
,当![]() ≥2时,
≥2时,![]() ,两式相减整理得
,两式相减整理得![]() ,再求出
,再求出![]() ,进而说明数列
,进而说明数列![]() 是等比数列,求出
是等比数列,求出![]() ,设正项等差数列
,设正项等差数列![]() 的公差为
的公差为![]() ,由已知条件求出
,由已知条件求出![]() ,进而求得
,进而求得![]() ;
;
(2)由(1)求得![]() ,再求
,再求![]() ,即可证明结论.
,即可证明结论.
(1)解法一:选择①②
当![]() 时,由
时,由![]() 得
得
![]() ,
,
两式相减,得![]() ,即
,即![]() ,
,
由①得![]() ,即
,即![]() ,
,
∴![]() ,得
,得![]() ,
,
∴![]() ,∴
,∴![]() 为
为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
∴![]() .
.
设等差数列![]() 的公差为
的公差为![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
![]() ,即
,即![]() ,
,
解得![]() ,
,![]() (舍去),∴
(舍去),∴![]()
解法二:选择②③
当![]() 时,由③
时,由③![]() ,
,
得![]() ,
,
两式相减,得![]() ,∴
,∴![]() ,
,
又![]() ,得
,得![]() ,
,
∴![]() ,∴
,∴![]() 为
为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
∴![]() .
.
(以下同法一)
(2)证明:由(1)得![]()
则![]()
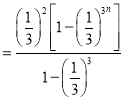
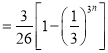
![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
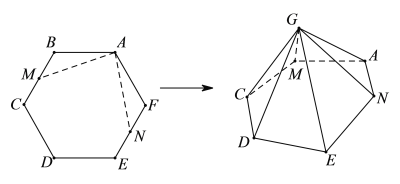
【题目】如图,六边形![]() 的六个内角均相等,
的六个内角均相等,![]() ,M,N分别是线段
,M,N分别是线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() ,现将
,现将![]() ,
,![]() 折起,使得B,F重合于点G,则二面角
折起,使得B,F重合于点G,则二面角![]() 的余弦值的取值范围是______.
的余弦值的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、“90后”从事互联网行业岗位分布条形图,则下列结论中正确的是( )
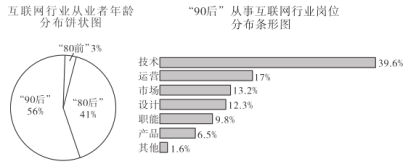
注:“90后”指1990年及以后出生的人,“80后”指1980-1989年之间出生的人,“80前”指1979年及以前出生的人.
A.互联网行业从业人员中“90后”占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数“90后”比“80前”多
D.互联网行业中从事技术岗位的人数“90后”比“80后”多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:过椭圆上的一点(不与长轴的端点重合)与椭圆的两个焦点确定的三角形称为椭圆的焦点三角形;已知过椭圆![]() 上一点P(不与长轴的端点重合)的焦点三角形
上一点P(不与长轴的端点重合)的焦点三角形![]() ,且
,且![]() .
.
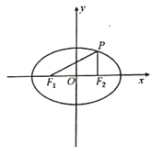
(1)求证:焦点三角形![]() 的面积为定值
的面积为定值![]() ;
;
(2)已知椭圆![]() 的一个焦点三角形为
的一个焦点三角形为![]() ,
,![]() ;
;
①若![]() ,求
,求![]() 点的横坐标的范围;
点的横坐标的范围;
②若![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,记
,记![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日上午,庆祝中华人民共和国成立70周年阅兵仪式在天安门广场隆重举行,这次阅兵不仅展示了我国的科技军事力量,更是让世界感受到了中国的日新月异,去年的阅兵方阵有一个很抢眼,他们就是院校科研方阵,他们是由军事科学院,国防大学,国防科技大学联合组建,若已知甲,乙,丙三人来自上述三所学校,学位分别有学士、硕士、博士学位,现知道:①甲不是军事科学院的,②来自军事科学院的均不是博士,③乙不是军事科学院的,④乙不是博士学位,⑤来自国防科技大学的是硕士,则甲是来自哪个院校的,学位是什么( )
A.国防大学,博士B.国防科技大学,硕士
C.国防大学,学士D.军事科学院,学士
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com