
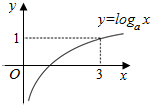
| A. |  | B. | 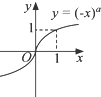 | C. | 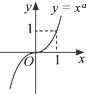 | D. | 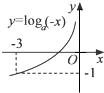 |
分析 分别同函数图象过已知点,求出a的值,即可得到答案.
解答 解:由图象可知,函数y=logax(a>0,且a≠1)的图象过点(3,1),
∴loga3=1,
解得a=3,
对于选项A:图象过点(1,3),则3=a-1,解得a=$\frac{1}{3}$,
对于选项B,图象过点(1,1),则1=(-1)a,解得a为偶数,
对于选项C,图象过点(1,1),则1=1a,解得a任意数,
对于选项D,图象过点(-3,-1),则-1=loga3,解得a=$\frac{1}{3}$,
综上所述,只有C的图象正确.
故选:C
点评 本题考查了函数的图象的识别,关键是通过已知点,求出参数a的值,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
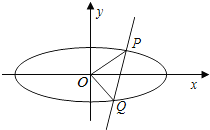 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
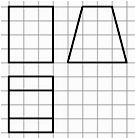
| A. | 42+6$\sqrt{17}$ | B. | 30+6$\sqrt{17}$ | C. | 66 | D. | 44 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,2) | B. | (1,$\sqrt{2}$] | C. | (0,$\sqrt{2}$] | D. | [$\frac{{\sqrt{2}}}{2}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{3}x+3\sqrt{3}$+2 | B. | y=$\frac{{\sqrt{3}}}{3}x+\sqrt{3}$+2 | C. | y=$\sqrt{3}x-3\sqrt{3}$-2 | D. | y=$\frac{{\sqrt{3}}}{3}x-\sqrt{3}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N=R | B. | M∩N=∅ | C. | CuN=M | D. | CvM⊆N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3-2ln2}{4}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com